«K12/K13» Geraden «PDF», «POD»

0.1 ↑ Geometrie

0.1.1 ↑ Geraden

0.1.1.1 ↑ Ursprungsgeraden in der x_1$x_1$–x_2$x_2$-Ebene

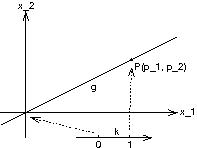
Liegt Q(q_1, q_2)$Q\left(q_1,q_2\right)$ auf g$g$?

Q(q_1, q_2) \in g$Q\left(q_1,q_2\right)\in g$ ⇔ Es gibt eine Zahl k \in \mathds{R}$k\in \mathbb{ℝ}$, so dass gilt:

q_1 = k p_1 \wedge q_2 = k p_2;$q_1=k{p}_1\wedge q_2=k{p}_2;$

Anders geschrieben:

\begin{pmatrix}q_1 \\ q_2\end{pmatrix} = k \begin{pmatrix}p_1 \\ p_2\end{pmatrix}\!;$\left(\begin{array}{c}\hfill q_1\hfill \\ \hfill q_2\hfill \end{array}\right)=k\left(\begin{array}{c}\hfill p_1\hfill \\ \hfill p_2\hfill \end{array}\right);$

Darstellung von g$g$:

g = \left\{ Q(q_1,q_2) \middle| \begin{pmatrix}q_1\\q_2\end{pmatrix} = k \begin{pmatrix}p_1\\p_2\end{pmatrix} \text{mit }k \in \mathds{R} \right\}\!;$g=\left\{Q\left(q_1,q_2\right)\mid \left(\begin{array}{c}\hfill q_1\hfill \\ \hfill q_2\hfill \end{array}\right)=k\left(\begin{array}{c}\hfill p_1\hfill \\ \hfill p_2\hfill \end{array}\right)\text{mit }k\in \mathbb{ℝ}\right\};$

0.1.1.2 ↑ Ursprungsgeraden im Raum

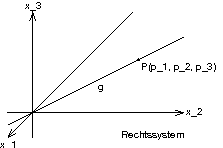
g = \left\{ Q(q_1,q_2,q_3) \middle| \begin{pmatrix}q_1\\q_2\\q_3\end{pmatrix} = k \begin{pmatrix}p_1\\p_2\\p_3\end{pmatrix} \text{mit }k \in \mathds{R} \wedge p_1^2 + p_2^2 + p_3^2 \neq 0 \right\}\!;$g=\left\{Q\left(q_1,q_2,q_3\right)\mid \left(\begin{array}{c}\hfill q_1\hfill \\ \hfill q_2\hfill \\ \hfill q_3\hfill \end{array}\right)=k\left(\begin{array}{c}\hfill p_1\hfill \\ \hfill p_2\hfill \\ \hfill p_3\hfill \end{array}\right)\text{mit }k\in \mathbb{ℝ}\wedge p_1^2+p_2^2+p_3^2\ne 0\right\};$

0.1.1.3 ↑ Beliebige Geraden in der x_1$x_1$–x_2$x_2$-Ebene

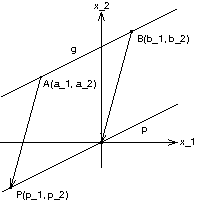
Abbildung: \\$$ g \to p$g\to p$ \\$$ B \mapsto 0$B\mapsto 0$ \\$$ A \mapsto P$A\mapsto P$

Welche Koordinaten hat P$P$?

p_1 = a_1 - b_1;$p_1=a_1-b_1;$ \\$$ p_2 = a_2 - b_2;$p_2=a_2-b_2;$

p = \left\{ Q(q_1, q_2) \middle| \begin{pmatrix}q_1\\q_2\end{pmatrix} = k \begin{pmatrix}a_1 - b_1\\a_2 - b_2\end{pmatrix} \text{mit } k \in \mathds{R} \right\}\!;$p=\left\{Q\left(q_1,q_2\right)\mid \left(\begin{array}{c}\hfill q_1\hfill \\ \hfill q_2\hfill \end{array}\right)=k\left(\begin{array}{c}\hfill a_1-b_1\hfill \\ \hfill a_2-b_2\hfill \end{array}\right)\text{mit }k\in \mathbb{ℝ}\right\};$

g = \left\{ R(r_1, r_2) \middle| \begin{pmatrix}r_1\\r_2\end{pmatrix} = k \begin{pmatrix}a_1 - b_1\\a_2 - b_2\end{pmatrix} + \begin{pmatrix}b_1\\b_2\end{pmatrix} = \begin{pmatrix}b_1\\b_2\end{pmatrix} + k \begin{pmatrix}a_1 - b_1\\a_2 - b_2\end{pmatrix} \text{mit } k \in \mathds{R} \right\}\!;$g=\left\{R\left(r_1,r_2\right)\mid \left(\begin{array}{c}\hfill r_1\hfill \\ \hfill r_2\hfill \end{array}\right)=k\left(\begin{array}{c}\hfill a_1-b_1\hfill \\ \hfill a_2-b_2\hfill \end{array}\right)+\left(\begin{array}{c}\hfill b_1\hfill \\ \hfill b_2\hfill \end{array}\right)=\left(\begin{array}{c}\hfill b_1\hfill \\ \hfill b_2\hfill \end{array}\right)+k\left(\begin{array}{c}\hfill a_1-b_1\hfill \\ \hfill a_2-b_2\hfill \end{array}\right)\text{mit }k\in \mathbb{ℝ}\right\};$

[Verschiedene Sichten: Die Sicht vor dem letzten Gleichheitszeichen stellt man sich durch eine Verschiebung jedes Punkten der Ursprungsgeraden vor. Das Ergebnis der Verschiebung ist dann die resultierende Gerade. Die Sicht nach dem letzten Gleichheitszeichen ist die bevorzugte Sicht. Bei ihr stellt man sich vor, dass man vom Ursprung ausgehend zum Aufpunkt (B$B$) geht und dann von dort aus jeweils das k$k$-fache des Richtungsvektors \left(\!\begin{smallmatrix}a_1 - b_1\\a_2 - b_2\end{smallmatrix}\!\right)$\left(\begin{array}{c}{a}_1-b_1\\ a_2-b_2\end{array}\right)$ aufträgt.]

Ein Zahlenpaar \left(\!\begin{smallmatrix}e\\f\end{smallmatrix}\!\right)$\left(\begin{array}{c}e\\ f\end{array}\right)$ kann durch Pfeile veranschaulicht werden, deren x_1$x_1$-Koordinate e$e$ und deren x_2$x_2$-Koordinate f$f$ ist.

Diese Pfeile sind alle parallel, gleich gerichtet und gleich lang zum Pfeil \overrightarrow{0W}$\overrightarrow{0W}$ mit W(e, f)$W\left(e,f\right)$.

(Diese Eigenschaft nennt man Parallelgleichheit.)

Die Menge aller parallelgleichen Pfeile heißt Pfeilvektor. Jedes Element, d.h. jeder Pfeil, dieser Menge heißt Repräsentant dieser Menge.

Bezeichnungen: \vec a = \overrightarrow{PQ} = \left(\!\begin{smallmatrix}2\\-3\end{smallmatrix}\!\right) = \left(\!\begin{smallmatrix}q_1 - p_1\\q_2 - p_2\end{smallmatrix}\!\right) \equiv \left(\!\begin{smallmatrix}q_1\\q_2\end{smallmatrix}\!\right) - \left(\!\begin{smallmatrix}p_1\\p_2\end{smallmatrix}\!\right) = \overrightarrow{0Q} - \overrightarrow{0P} \equiv \vec Q - \vec P$\overrightarrow{a}=\overrightarrow{PQ}=\left(\begin{array}{c}2\\ -3\end{array}\right)=\left(\begin{array}{c}{q}_1-p_1\\ q_2-p_2\end{array}\right)\equiv \left(\begin{array}{c}{q}_1\\ q_2\end{array}\right)-\left(\begin{array}{c}{p}_1\\ p_2\end{array}\right)=\overrightarrow{0Q}-\overrightarrow{0P}\equiv \overrightarrow{Q}-\overrightarrow{P}$

PQ = \left\{ X(x_1, x_2) \middle| \left(\!\begin{smallmatrix}x_1\\x_2\end{smallmatrix}\!\right) = \vec P + k \overrightarrow{PQ} \text{ mit } k \in \mathds{R} \right\}\!;$PQ=\left\{X\left(x_1,x_2\right)\mid \left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)=\overrightarrow{P}+k\overrightarrow{PQ}\text{ mit }k\in \mathbb{ℝ}\right\};$

Kürzer: PQ{:}\, \vec X = \vec P + k \overrightarrow{PQ}; \quad$PQ:\overrightarrow{X}=\overrightarrow{P}+k\overrightarrow{PQ};$ (k \in \mathds{R}$k\in \mathbb{ℝ}$)

0.1.1.4 ↑ Möglichkeiten der gegenseitigen Lage zweier Geraden g$g$ und h$h$ in der Ebene

g{:}\, \vec X = \vec A + k \vec u; \quad k \in \mathds{R};$g:\overrightarrow{X}=\overrightarrow{A}+k\overrightarrow{u};k\in \mathbb{ℝ};$ \\$$ h{:}\, \vec X = \vec B + l \vec v; \quad l \in \mathds{R};$h:\overrightarrow{X}=\overrightarrow{B}+l\overrightarrow{v};l\in \mathbb{ℝ};$

• g$g$ und h$h$ schneiden sich (in einem Punkt).

  ⇔ Es gibt kein r \in \mathds{R}$r\in \mathbb{ℝ}$, so dass \vec u = r \vec v$\overrightarrow{u}=r\overrightarrow{v}$, d.h. \vec u$\overrightarrow{u}$ und \vec v$\overrightarrow{v}$ sind keine Vielfache voneinander. (\vec u$\overrightarrow{u}$ und \vec v$\overrightarrow{v}$ heißen dann nicht kollinear, d.h. die Repräsentanten von \vec u$\overrightarrow{u}$ sind nicht parallel zu den Repräsentanten von \vec v$\overrightarrow{v}$.)

  Bestimmung des Schnittspunkts: Der Schnittpunkt erfüllt sowohl die Gleichung von g$g$ (für ein bestimmtes k$k$) als auch die Gleichung von h$h$ (für ein bestimmtes l$l$).

  \left.\begin{array}{@{}l} {} \vec S = \vec A + k_S \vec u; \\ {} \vec S = \vec B + l_S \vec v; \end{array}\right\}\Rightarrow {} \vec A + k_S \vec u = \vec B + l_s \vec v;$\left.\begin{array}{c}\overrightarrow{S}=\overrightarrow{A}+k_S\overrightarrow{u};\hfill \\ \overrightarrow{S}=\overrightarrow{B}+l_S\overrightarrow{v};\hfill \end{array}\right\}\Rightarrow \overrightarrow{A}+k_S\overrightarrow{u}=\overrightarrow{B}+l_s\overrightarrow{v};$

• g$g$ und h$h$ sind parallel [⇔ die Richtungsvektoren sind kollinear].

  • g$g$ und h$h$ sind identisch [⇔ der Verbindungsvektor ist kollinear zu den Richtungsvektoren].

  • g$g$ und h$h$ sind echt parallel [⇔ der Verbindungsvektor ist nicht kollinear zu den Richtungsvektoren].

0.1.1.5 ↑ Beliebige Geraden im Raum

g{:}\, \vec X = \vec A + k \overrightarrow{AB}; \quad k \in \mathds{R};$g:\overrightarrow{X}=\overrightarrow{A}+k\overrightarrow{AB};k\in \mathbb{ℝ};$

0.1.1.6 ↑ Möglichkeiten der gegenseitigen Lage zweier Geraden g$g$ und h$h$ im Raum

g{:}\, \vec X = \vec A + k \vec u; \quad k \in \mathds{R};$g:\overrightarrow{X}=\overrightarrow{A}+k\overrightarrow{u};k\in \mathbb{ℝ};$ \\$$ h{:}\, \vec X = \vec B + l \vec v; \quad l \in \mathds{R};$h:\overrightarrow{X}=\overrightarrow{B}+l\overrightarrow{v};l\in \mathbb{ℝ};$

• g$g$ und h$h$ sind parallel. ⇔ \vec u$\overrightarrow{u}$ und \vec v$\overrightarrow{v}$ sind kollinear.

  Wenn g$g$ und h$h$ parallel sind, gilt:

  A \in h$A\in h$ ⇔ g$g$ und h$h$ identisch ⇔ \overrightarrow{AB}$\overrightarrow{AB}$ und \vec u$\overrightarrow{u}$ [oder \vec v$\overrightarrow{v}$] kollinear

• (Wenn g$g$ und h$h$ nicht parallel sind, gilt:)

  g$g$ und h$h$ schneiden sich ⇔ die Gleichung \vec A + k \vec u = \vec B + l \vec v$\overrightarrow{A}+k\overrightarrow{u}=\overrightarrow{B}+l\overrightarrow{v}$ hat für k$k$ und l$l$ genau eine Lösung, d.h. es gibt genau einen Wert für k$k$ und genau einen Wert für l$l$, sodass die Gleichung erfüllt ist.

0.1.1.7 ↑ Vorgehen bei einem System aus drei Gleichungen für zwei Lö­sungs­va­ri­a­blen

1. Eine Gleichung wird nach einer Lösungsvariablen aufgelöst.

2. Der erhaltene Term wird in eine weitere Gleichung eingesetzt.

3. Man versucht, für die zweite Lösungsvariante einen Term zu bestimmen. [Falls das nicht gelingt, hat das Gleichungssystem keine Lösung.]

4. Falls für beide Lösungsvariablen Terme gefunden wurden, muss überprüft werden, ob auch die restliche Gleichung damit er­füllt ist.

0.1.1.8 ↑ Teilverhältnis

•  --------+-----+-----+--------

•          A     T₁    B

[T_1$T_1$ Mittelpunkt von \left[AB\right]$\left[AB\right]$]

\overrightarrow{AT} = \lambda \overrightarrow{TB};$\overrightarrow{AT}=\lambda \overrightarrow{TB};$

• T \in AB \setminus \left[AB\right.$T\in AB\setminus \left[AB\right.$: \lambda \in \left]-1, 0\right[;$\lambda \in \left]-1,0\right[;$

• T = A$T=A$: \lambda = 0;$\lambda =0;$

• T \in \left[A T_1\right] \setminus \left\{ A, T_1 \right\}$T\in \left[A{T}_1\right]\setminus \left\{A,T_1\right\}$: \lambda \in \left]0, 1\right[;$\lambda \in \left]0,1\right[;$

• T = T_1$T=T_1$: \lambda = 1;$\lambda =1;$

• T \in \left[T_1 B\right] \setminus \left\{ T_1, B \right\}$T\in \left[T_{1}B\right]\setminus \left\{T_1,B\right\}$: \lambda \in \left]1, \infty\right[;$\lambda \in \left]1,\infty \right[;$

• [T = B$T=B$: \lambda$\lambda$ undefiniert]

• [T \in AB \setminus \left.AB\right]$T\in AB\setminus \left.AB\right]$: \lambda \in \left]-\infty, -1\right[;$\lambda \in \left]-\infty ,-1\right[;$]

\lambda = \lambda(T);$\lambda =\lambda \left(T\right);$

\lambda(0) = 0;$\lambda \left(0\right)=0;$

\lambda = \frac{T - A}{B - T} = \frac{T}{B - T};$\lambda =\frac{T-A}{B-T}=\frac{T}{B-T};$

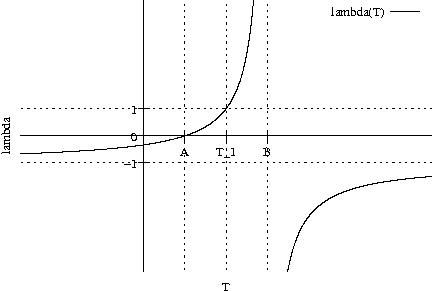
Festlegung: A$A$, B$B$, T$T$ liegen auf einer Geraden. T$T$ teilt \left[AB\right]$\left[AB\right]$ im Verhältnis \lambda$\lambda$. ⇔ \overrightarrow{AT} = \lambda \overrightarrow{TB};$\overrightarrow{AT}=\lambda \overrightarrow{TB};$

0.1.1.9 ↑ Abstand einer Geraden zu einem Punkt

\overrightarrow{PS} \cdot \vec u = 0;$\overrightarrow{PS}\cdot \overrightarrow{u}=0;$

\left(\underbrace{\vec A + k_S \vec u}_{\vec S} - \vec P\right) \cdot \vec u = 0;$\left(\underset{\overrightarrow{S}}{\underbrace{\overrightarrow{A}+k_S\overrightarrow{u}}}-\overrightarrow{P}\right)\cdot \overrightarrow{u}=0;$ (Gleichung für k_s$k_s$)

0.1.1.10 ↑ Abstand zweier Geraden

g{:}\, \vec X = \vec A + k \vec u; \quad k \in \mathds{R};$g:\overrightarrow{X}=\overrightarrow{A}+k\overrightarrow{u};k\in \mathbb{ℝ};$

h{:}\, \vec X = \vec B + l \vec v; \quad l \in \mathds{R};$h:\overrightarrow{X}=\overrightarrow{B}+l\overrightarrow{v};l\in \mathbb{ℝ};$

d(g,h) = \left|\overrightarrow{PQ}\right|$d\left(g,h\right)=\left|\overrightarrow{PQ}\right|$ mit P \in g$P\in g$ und Q \in h$Q\in h$ und \left[PQ\right] \perp g$\left[PQ\right]\perp g$ und \left[PQ\right] \perp h$\left[PQ\right]\perp h$.

\vec P = \vec A + k_P \vec u; \quad \overrightarrow{PQ} \cdot \vec u = 0;$\overrightarrow{P}=\overrightarrow{A}+k_P\overrightarrow{u};\overrightarrow{PQ}\cdot \overrightarrow{u}=0;$

\vec Q = \vec B + l_Q \vec v; \quad \overrightarrow{PQ} \cdot \vec v = 0;$\overrightarrow{Q}=\overrightarrow{B}+l_Q\overrightarrow{v};\overrightarrow{PQ}\cdot \overrightarrow{v}=0;$

\left(\vec B + l_Q \vec v - \vec A - k_P \vec u\right) \cdot \vec u = 0;$\left(\overrightarrow{B}+l_Q\overrightarrow{v}-\overrightarrow{A}-k_P\overrightarrow{u}\right)\cdot \overrightarrow{u}=0;$

\left(\vec B + l_Q \vec v - \vec A - k_P \vec u\right) \cdot \vec v = 0;$\left(\overrightarrow{B}+l_Q\overrightarrow{v}-\overrightarrow{A}-k_P\overrightarrow{u}\right)\cdot \overrightarrow{v}=0;$