0.0.1 ↑ Ebenen
Echt parallele Geraden mit Aufpunkt auf g bestimmen eine Ebene E.
E = \left\{ X \middle| \vec X = \vec A_l + k \vec u \text{ mit } k \in \mathds{R} \wedge \vec A_l = \vec B + l \vec v \text{ mit } l \in \mathds{R} \wedge \left\{ \vec u, \vec v \right\} \text{nicht kollinear} \right\}\!;
Kürzer:
E{:}\, \vec X = \vec B + k \vec u + l \vec v; \quad k, l \in \mathds{R};
0.0.1.1 ↑ Möglichkeiten der gegenseitigen Lage von Gerade und Ebene
E{:}\, \vec X = \vec P + k \vec u + l \vec v;
g{:}\, \vec X = \vec Q + r \vec w;
g und E sind parallel. ⇔
Es gibt Repräsentanten der Richtungsvektoren, die in einer [gemeinsamen] Ebene liegen.
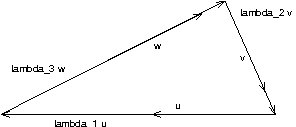
\lambda_1 \vec u + \lambda_2 \vec v + \lambda_3 \vec w = \vec 0;
Dabei sind nicht alle \lambda_i, i = 1, 2, 3 zugleich Null. (\lambda_1^2 + \lambda_2^2 + \lambda_3^2 \neq 0;)
[D.h.] \vec u, \vec v, \vec w sind komplanar.
[g \subset E ⇔ die Richtungsvektoren sind komplanar und \text{Aufpunkt} \in E]
\vec P + k \vec u + l \vec v = \vec Q + r \vec w;
E und g echt parallel ⇔ die Gleichung hat keine Lösung;
g \subset E ⇔ die Gleichung hat unendlich viele Lösungen ("die Punkte von g")
g und E schneiden sich in einem Punkt ⇔ die Gleichung hat genau eine Lösung;]
0.0.1.2 ↑ Möglichkeiten der gegenseitigen Lage zweier Ebenen
Beide Ebenen sind in vektorieller Parameterform gegeben.
E{:}\, \vec X = \vec A + k \vec u + l \vec v; \quad k, l \in \mathds{R}; \quad {}F{:}\, \vec X = \vec B + m \vec w + n \vec z; \quad m, n \in \mathds{R};
E und F sind parallel. ⇔
\vec u, \vec v, \vec w, \vec z sind komplanar. ⇔
\vec u, \vec v, \vec w und \vec u, \vec v, \vec z sind komplanar.
E und F ist echt parallel. ⇔
E \parallel F und \left[\left(A \not\in F\right) \vee \left(B \not\in E\right) \vee \left(\overrightarrow{AB}\text{, }\vec u\text{, }\vec v\text{ nicht komplanar}\right)\right].
E und F sind identisch. ⇔
E \parallel F und \left[\left(A \in F\right) \vee \left(B \in E\right) \vee \left(\overrightarrow{AB}\text{, }\vec u\text{, }\vec v\text{ komplanar}\right)\right]. ⇔
\vec A + k \vec u + l \vec v = \vec B + m \vec w + n \vec z; hat eine Lösungsmenge mit zwei frei wählbaren Lösungsvariablen (Ebenengleichung).
E und F schneiden sich in einer Geraden. ⇔ E \nparallel F;
[BTW]
E \cap F = \varnothing: Beim Versuch, die Lösung zu finden, tritt ein Widerspruch auf.
E \cap F = \text{Gerade }g: Lösungsmenge mit einer frei wählbaren Variable.
E \cap F = E = F: [Lösungsmenge mit zwei frei wählbaren Variablen.]
Eine Ebene ist in Parameter-, eine in Koordinatenform gegeben.
E{:}\, a x_1 + b x_2 + c x_3 + d = 0; \quad {}F{:}\, \text{[}\vec X = \vec B + m \vec w + n \vec z; \quad m, n \in \mathds{R};\text{]}
Einsetzen von x_1, x_2, x_3 aus der Gleichung von F in die Gleichung von E ergibt eine Gleichung (∗) für m und n.
E und F [sind] identisch. ⇔ m und n sind frei wählbar bezüglich (∗).
E und F sind echt parallel. ⇔ (∗) ist nicht lösbar.
E und F schneiden sich [in einer Gerade]. ⇔ Die Lösungsmenge hat eine frei wählbare Variable; m = m(n); n = n(m) [XXX IMHO ist diese Notation mathematisch unsinnig – m bzw. n können nicht eine Funktion (von \mathds{R} nach \mathds{R}) und eine reelle Zahl zugleich sein.]
[Beide Ebenen sind in Koordinatenform gegeben.]
\left.\begin{array}{@{}l} {} E{:}\, a x_1 + b x_2 + c x_3 + d = 0; \\ {} F{:}\, \alpha x_1 + \beta x_2 + \gamma x_3 + \delta = 0; \end{array}\right\} \text{Gleichungssystem für }x_1,x_2,x_3
[E und F sind identisch. ⇔ Gleichung von E ist ein Vielfaches von der von F.]
[E und F sind echt parallel. ⇔ Die Koeffizienten von E sind Vielfache von denen von F, aber d \neq \delta.]
[E und F schneiden sich in einer Geraden. ⇔ Die Koeffizienten von E sind nicht Vielfache von denen von F.]
0.0.1.3 ↑ [Winkel zwischen Ebene und Gerade/Normal(en)form einer Ebene
\angle(E,g) = \angle(p,g);
\vec u, \vec v: Richtungsvektoren von E
\vec n \perp E;
\vec n \cdot \vec u = \vec n \cdot \vec v = 0;]
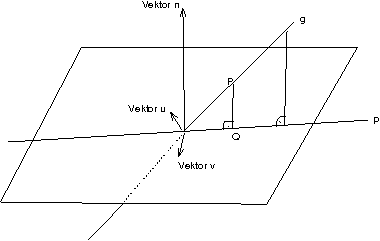
X \in E; ⇔ \vec n \cdot \overrightarrow{AX} = 0;
\vec n \cdot \left(\vec X - \vec A\right) = 0; (vektorielle Normalform einer Ebene)
\left(\!\begin{smallmatrix}n_1\\n_2\\n_3\end{smallmatrix}\!\right) \left[\left(\!\begin{smallmatrix}x_1\\x_2\\x_3\end{smallmatrix}\!\right) - \left(\!\begin{smallmatrix}a_1\\a_2\\a_3\end{smallmatrix}\!\right)\right] = n_1 x_1 + n_2 x_2 + n_3 x_3 \underbrace{- \left(n_1 a_1 + n_2 a_2 + n_3 a_3\right)}_{n_0} = n_1 x_1 + n_2 x_2 + n_3 x_3 + n_0 = 0; (skalare Normalform/Koordinatenform einer Ebene)
\vec n \cdot \overrightarrow{AX} > 0; → \vec X liegt bezüglich \vec n im oberen (positiven) Halbraum
"na langsam wird halt doch sichtbar, dass die Mathematik eine Universalwissenschaft ist"
0.0.1.3.1 ↑ [Hesse-Normierungen]
0.0.1.3.1.1 ↑ 1. Hesse-Normierung für \text{Ursprung} \not\in E
Ursprung im unteren Halbraum, d.h. \vec n \vec A > 0.
Senkrechte Projektion von \overrightarrow{AX} auf die Richtung von \vec n ergibt den Abstand von X zur Ebene.
d(X,E) = \left|\overrightarrow{AX}\right| \underbrace{\left|\frac{\vec n}{\left|\vec n\right|}\right|}_{1} \cdot \cos \underbrace{\angle\!\left(\vec n, \overrightarrow{AX}\right)}_{\angle\!\left(\frac{\vec n}{\left|\vec n\right|}, \overrightarrow{AX}\right)} = \overrightarrow{AX} \cdot \vec n^0 = \vec n^0 \cdot \left(\vec X - \vec A\right) > 0 für X im oberen Halbraum.
d(X,E) = \left|\overbrace{\underbrace{\vec n_0}_{\text{HESSEvektor}} \cdot \overrightarrow{AX}}^{\text{HESSEterm (HT)}}\right|;
0.0.1.3.1.2 ↑ 2. Hesse-Normierung
Der Normalenvektor soll die Länge 1 haben.
HT(X) = 0; ⇔ X \in E;
HT(X) < 0; ⇔ X und Ursprung liegen im gleichen Halbraum
0.0.1.3.2 ↑ HESSEnormalform einer Ebene (HNF)
HT(X) = \vec n_0 \cdot \left(\vec X - \vec A\right) = \vec n_0 \vec X - \vec n_0 \vec A = 0 mit \left|\vec n_0\right| = 1 und \vec n_0 \cdot \vec A > 0;
0.0.1.3.2.3 ↑ Umschreiben der Normalform in die HESSEnormalform
[Normalform:] \vec n \vec X - \vec n \vec A = 0;
[HESSEnormalform:] \dfrac{\vec n \vec X - \vec n \vec A}{\left|\vec n\right| \cdot \operatorname{sgn} \vec n \vec A} = 0;