0.0.1 ↑ Kreise
0.0.1.1 ↑ Satz des Thales
"na du musst nur 'ne längere Zeit als Photon leben, dann wird's dir schon klar werden..."
"glaub mir, ich spreche aus Erfahrung"
"Du setzt dich aufs Fahrrad, fährst so schnell, dass es dunkel wird, und schaust dann auf den Tacho"
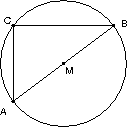
Für ein Dreieck ABC sind die beiden folgenden Aussagen äquivalent:
- (1)
Der Innenwinkel bei C ist 90^\circ.
- (2)
C liegt auf dem Kreis über \left[AB\right].
Beweis:
M sei der Mittelpunkt von \left[AB\right].
\renewcommand{\arraystretch}{1.5}\begin{array}{rcll} {} && \text{(1)} & \Leftrightarrow \\ {} \overrightarrow{CA} \cdot \overrightarrow{CB} &=& 0; \quad & \Leftrightarrow \\ {} \left(\overrightarrow{CM} + \overrightarrow{MA}\right) \cdot {} \left(\overrightarrow{CM} + \overrightarrow{MB}\right) &=& 0; \quad & \Leftrightarrow \\ {} \left(\overrightarrow{CM} + \overrightarrow{MA}\right) \cdot {} \left(\overrightarrow{CM} - \overrightarrow{MA}\right) &=& 0; \quad & \Leftrightarrow \\ {} {\overrightarrow{CM}}^2 - {\overrightarrow{MA}}^2 &=& 0; \quad & \Leftrightarrow \\ {} {\overrightarrow{CM}}^2 &=& {\overrightarrow{MA}}^2; \quad & \Leftrightarrow \\ {} \left|\overrightarrow{CM}\right|^2 &=& \left|\overrightarrow{MA}\right|^2; \quad & \Leftrightarrow \\ {} \left|\overrightarrow{CM}\right| &=& \left|\overrightarrow{MA}\right|; \quad & \Leftrightarrow \text{(2)} \end{array}