«K12/K13» 119. Hausaufgabe «PDF», «POD»

0.0.1 ↑ 119. Hausaufgabe

0.0.1.1 ↑ Analysis-Buch Seite 258, Aufgabe 32

f(x) = \ln\!\left(x^2 + 4\right);$f\left(x\right)=ln\left(x^2+4\right);$

a)

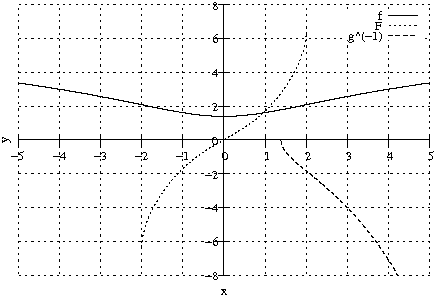
Diskutiere f$f$ und zeichne G_f$G_f$.

f(x) \stackrel{!}{=} 0;$f\left(x\right)\stackrel{!}{=}0;$ → keine Nullstellen

f(-x) = f(x);$f\left(-x\right)=f\left(x\right);$ → Symmetrie zur y$y$-Achse

\lim\limits_{x \to \pm\infty} f(x) = \infty;$\underset{x\to \pm \infty }{lim}f\left(x\right)=\infty ;$

f'(x) = \frac{2 x}{x^2 + 4} \stackrel{!}{=} 0;$f^{\prime }\left(x\right)=\frac{2x}{x^2+4}\stackrel{!}{=}0;$ → TIP bei (0,\ln 4);$\left(0,ln4\right);$

f''(x) = \frac{-2x^2 + 8}{\left(x^2 + 4\right)^2} = -2 \cdot \frac{\left(x - 2\right) \left(x + 2\right)}{\left(x^2 + 4\right)^2} \stackrel{!}{=} 0;$f^{\prime \prime }\left(x\right)=\frac{-2x^2+8}{{\left(x^2+4\right)}^2}=-2\cdot \frac{\left(x-2\right)\left(x+2\right)}{{\left(x^2+4\right)}^2}\stackrel{!}{=}0;$ → WEP bei (\pm 2, \ln 8);$\left(\pm 2,ln8\right);$

b)

Berechne den Inhalt der Fläche A$A$ zwischen G_f$G_f$ und der Verbindungsgeraden seiner Wendepunkte. Wie verhält sich A$A$ zur Fläche jenes Rechtecks, das der Fläche A$A$ umschrieben ist?

Wie verhält sich A$A$ zur Fläche des umbeschriebenen gleichschenkligen Dreiecks, dessen Schenkel auf den Wendetangenten liegen?

\int \ln\!\left(x^2 + 4\right) \cdot x' \,\mathrm{d}x = {}x \ln\!\left(x^2 + 4\right) - \int \underbrace{\frac{1}{x^2 + 4} \cdot 2x \cdot x}_{\frac{2x^2}{x^2 + 4}} \,\mathrm{d}x = \\ {}\quad = {}x \ln\!\left(x^2 + 4\right) - \int 2 \,\mathrm{d}x + \int \underbrace{\frac{8}{x^2 + 4}}_{\frac{2}{1 + \left(x/2\right)^2}} \,\mathrm{d}x = \\ {}\quad = {}x \ln\!\left(x^2 + 4\right) - 2x + 4 \int \frac{1/2}{1 + \left(x/2\right)^2} \,\mathrm{d}x = \\ {}\quad = {}x \ln\!\left(x^2 + 4\right) - 2x + 4 \arctan \frac{x}{2};$\int \; <!--nolimits-->ln\left(x^2+4\right)\cdot x^{\prime }\text{d}x=xln\left(x^2+4\right)-\int \; <!--nolimits-->\underset{\frac{2x^2}{x^2+4}}{\underbrace{\frac{1}{x^2+4}\cdot 2x\cdot x}}\text{d}x==xln\left(x^2+4\right)-\int \; <!--nolimits-->2\text{d}x+\int \; <!--nolimits-->\underset{\frac{2}{1+{\left(x∕2\right)}^2}}{\underbrace{\frac{8}{x^2+4}}}\text{d}x==xln\left(x^2+4\right)-2x+4\int \; <!--nolimits-->\frac{1∕2}{1+{\left(x∕2\right)}^2}\text{d}x==xln\left(x^2+4\right)-2x+4arctan\frac{x}{2};$

\int \ln 8 - \ln\!\left(x^2 + 4\right) \,\mathrm{d}x = 8 - 2 \pi;$\int \; <!--nolimits-->ln8-ln\left(x^2+4\right)\text{d}x=8-2\pi ;$

Rechteckinhalt: \left[2 - \left(-2\right)\right] \cdot \left(\ln 8 - \ln 4\right) = \ln 16;$\left[2-\left(-2\right)\right]\cdot \left(ln8-ln4\right)=ln16;$

Wendetangentenschnittpunkt: f'(\pm 2) = \pm \frac{1}{2};$f^{\prime }\left(\pm 2\right)=\pm \frac{1}{2};$ → Schnittpunkt bei \left(0,\ln 8 - 2 \cdot \frac{1}{2}\right) = (0,\ln 8 - 1);$\left(0,ln8-2\cdot \frac{1}{2}\right)=\left(0,ln8-1\right);$

Dreiecksinhalt: \frac{1}{2} \cdot \left[2 - \left(-2\right)\right] \cdot \left[\ln 8 - \left(\ln 8 - 1\right)\right] = 2;$\frac{1}{2}\cdot \left[2-\left(-2\right)\right]\cdot \left[ln8-\left(ln8-1\right)\right]=2;$

c)

g$g$ sei eine umkehrbare Einschränkung von f$f$ mit möglichst großer Definitionsmenge. G_g$G_g$ enthalte den Punkt (-1, ?)$\left(-1,?\right)$.

Bestimme g^{-1}$g^{-1}$ und stelle A$A$ durch ein Integral mit dem Integranden g^{-1}(x)$g^{-1}\left(x\right)$ dar. Substituiere darin x = \ln t^2$x=ln{t}^2$.

g(x) = \ln\!\left(x^2 + 4\right); \quad D_g = \mathds{R}_0^-; \quad W_g = \left[\ln 4, \infty\right[;$g\left(x\right)=ln\left(x^2+4\right);D_g={\mathbb{ℝ}}_0^{-};W_g=\left[ln4,\infty \right[;$

g(x) = y = \ln\!\left(x^2 + 4\right);$g\left(x\right)=y=ln\left(x^2+4\right);$ ⇔ x = -\sqrt{e^y - 4} = g^{-1}(y);$x=-\sqrt{e^y-4}=g^{-1}\left(y\right);$

Inhalt von A$A$, dargestellt über g^{-1}(x)$g^{-1}\left(x\right)$: -2 \int\limits_{f(0)}^{f(2)} g^{-1}(x) \,\mathrm{d}x = {}2 \int\limits_{f(0)}^{f(2)} \sqrt{e^x - 4} \,\mathrm{d}x = {}2 \int\limits_{t(f(0))}^{t(f(2))} \sqrt{e^{\ln t^2} - 4} \cdot \left(\ln t^2\right)' \,\mathrm{d}t = {}2 \int\limits_{t(f(0))}^{t(f(2))} \sqrt{t^2 - 4} \cdot \frac{1}{t^2} \cdot 2t \,\mathrm{d}t = {}4 \int\limits_{t(f(0))}^{t(f(2))} \frac{\sqrt{t^2 - 4}}{t} \,\mathrm{d}t$-2\underset{f\left(0\right)}{\overset{f\left(2\right)}{\int \; <!--nolimits-->}}{g}^{-1}\left(x\right)\text{d}x=2\underset{f\left(0\right)}{\overset{f\left(2\right)}{\int \; <!--nolimits-->}}\sqrt{e^x-4}\text{d}x=2\underset{t\left(f\left(0\right)\right)}{\overset{t\left(f\left(2\right)\right)}{\int \; <!--nolimits-->}}\sqrt{e^{ln{t}^2}-4}\cdot {\left(ln{t}^2\right)}^{\prime }\text{d}t=2\underset{t\left(f\left(0\right)\right)}{\overset{t\left(f\left(2\right)\right)}{\int \; <!--nolimits-->}}\sqrt{t^2-4}\cdot \frac{1}{t^2}\cdot 2t\text{d}t=4\underset{t\left(f\left(0\right)\right)}{\overset{t\left(f\left(2\right)\right)}{\int \; <!--nolimits-->}}\frac{\sqrt{t^2-4}}{t}\text{d}t$ mit t(x) = \sqrt{e^x};$t\left(x\right)=\sqrt{e^x};$