«K12/K13» 116. Hausaufgabe «PDF», «POD»

0.0.1 ↑ 116. Hausaufgabe

0.0.1.1 ↑ Zusammenfassung der Stunde: Lokalisierung und Delokalisierung

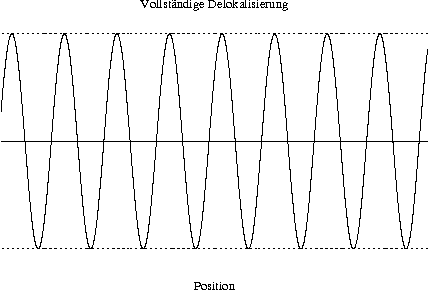
0.0.1.1.1 ↑ Vollständige Delokalisierung

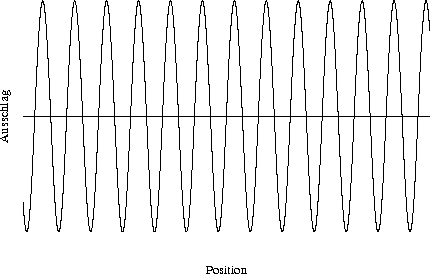
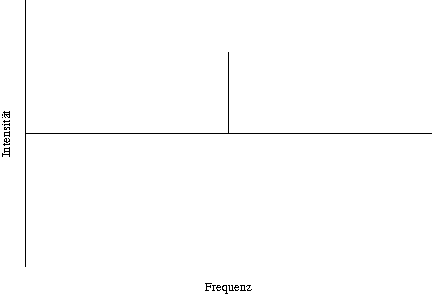
Vollständige Delokalisierung (unendliche Ortsunschärfe) wird mathematisch durch eine Sinus-Funktion fester Frequenz (Frequenzunschärfe Null) ausgedrückt.

Interpretiert man diese Funktion als Ton, so repräsentiert die Funktion einen unendlich lang ausgehaltenen, perfekten Sinuston genau einer Frequenz.

Anschaulich drückt sich die Delokalisierung dadurch aus, dass es unendlich viele Wellenberge gibt – es ist nicht klar, an welchem dieser Berge man den Ort festmachen sollte. Es gibt keinen Berg, dem man den Vorzug gegen könnte!

Über ein Elektron mit dieser Wellenfunktion könnte man also nicht sagen, wo es sich "aufhält" bzw. wo es sich manifestieren wird. Man kennt jedoch den Impuls (und damit die Geschwindigkeit) genau.

Bezogen auf die Unschärferelationen drückt sich dieser Sachverhalt wiefolgt aus:

\underbrace{\Delta f}_{0 \,\mathrm{Hz}} \cdot \underbrace{\Delta t}_{\infty \,\mathrm{s}} \geq c;$\underset{0\text{Hz}}{\underbrace{\Delta f}}\cdot \underset{\infty \text{s}}{\underbrace{\Delta t}}\ge c;$

\underbrace{\Delta p}_{0 \,\mathrm{Ns}} \cdot \underbrace{\Delta x}_{\infty \,\mathrm{m}} \geq c;$\underset{0\text{Ns}}{\underbrace{\Delta p}}\cdot \underset{\infty \text{m}}{\underbrace{\Delta x}}\ge c;$

Zu beachten ist, dass je nach Unschärferelation andere Größen, und damit auch andere Achsen auf dem Diagramm, vorkommen. Die beiden Diagramme oben beziehen sich auf die Ortsunschärfe.

Auch hat hier das \Delta$\Delta$-Symbol eine für uns unübliche Bedeutung: Hier bedeutet es die stochastische Standardabweichung, während es normalerweise eine Änderung einer Größe pro einer anderen Größe bezeichnet und somit auch nicht isoliert stehen darf: \frac{\Delta x}{\Delta t}$\frac{\Delta x}{\Delta t}$ ist zulässig, während \Delta x \Delta t$\Delta x\Delta t$ im für uns üblichen Sinne nicht zulässig ist, da nicht angegeben ist, auf welche anderen Größen sich \Delta x$\Delta x$ und \Delta t$\Delta t$ jeweils beziehen.

0.0.1.1.1.1 ↑ Unendlich mal Null = von Null verschiedener endlicher Wert? [FORMAL]

Formal ist außerdem zu beachten, dass weder das Vorkommen von Null im Produkt den Produktwert auf Null noch das Vorkommen von Unendlich den Produktwert auf Unendlich zwingt: Hinter der schlampigen Schreibweise stecken Grenzwertprozesse, die sich – anschaulich gesprochen – teilweise gegenseitig aufheben.

Da wir aber keine Formeln für die Werte der Unschärfen haben, können wir diesen Sachverhalt nicht näher analytisch untersuchen; das ist aber für das grundlegende anschauliche Verständnis auch nicht notwendig.

0.0.1.1.2 ↑ "Unvollständige" Delokalisierung

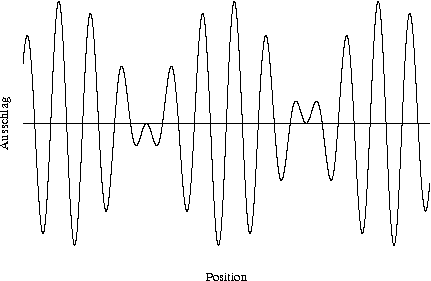
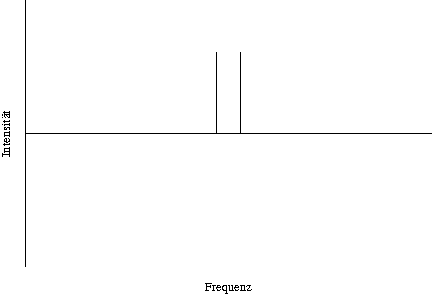
Man kann der vollständigen Delokalisierung Struktur hinzufügen. Dies modelliert man dadurch, indem man statt genau einer Frequenz \hat f$\widehat{f}$ ein diskretes Frequenzspektrum um \hat f$\widehat{f}$ nimmt, beispielsweise \hat f - \Delta f$\widehat{f}-\Delta f$ und \hat f + \Delta f$\widehat{f}+\Delta f$. (In diesem speziellen Fall kann \Delta f$\Delta f$ nicht nur als Standardabweichung, sondern auch unter dem für uns üblichen Sinn interpretiert werden.)

Als Ton interpretiert, wird das Signal periodisch (mit Periodendauer 1 / \Delta f$1∕\Delta f$) lauter und leiser ("Schwebung"). Es gibt also Momente, an denen das Signal ganz verschwindet, also die Amplitude Null ist; dadurch hat man die Strukturgebung erreicht.

Die Gesamtauslenkung ist also y = \sin \omega_1 x + \sin \omega_2 x$y=sin{\omega }_{1}x+sin{\omega }_{2}x$. Obwohl die Frage nach den Nullstellen dieses Terms nicht leicht zu beantworten ist, kann man zumindest einige Nullstellen – die "Stummpunkte" – analytisch bestimmen.

x$x$ ist nämlich dann ein "Stummpunkt", wenn beide Summanden zugleich Null sind.

Beispiel: f_1 = 440 \,\mathrm{Hz}; \quad f_2 = 441 \,\mathrm{Hz};$f_1=440\text{Hz};f_2=441\text{Hz};$

Nach jeweils einer Sekunde haben beide Sub-Oszillatoren eine ganze Schwingung vollendet; nach jeweils einer Sekunde sind beide Oszillatoren also wieder nicht ausgelenkt.

Bezogen auf die Unschärferelationen ist die Ortsunschärfe also nicht mehr Unendlich; stattdessen aber ist jetzt der Impuls unscharf.

Über ein Elektron mit dieser Wellenfunktion könnte man zwar nicht sagen, wo es sich manifestieren wird; es ist aber möglich, Manifestationswahrscheinlichkeiten anzugeben: An den "Stummpunkten" manifestiert es sich nie, und an den Punkten maximaler Amplitude am häufigsten.

0.0.1.1.3 ↑ "Nahezu vollständige" Delokalisierung

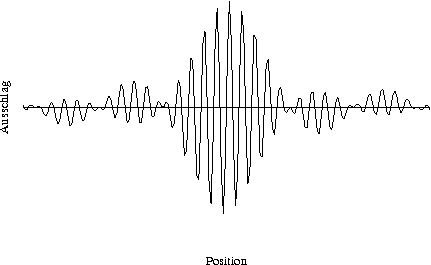
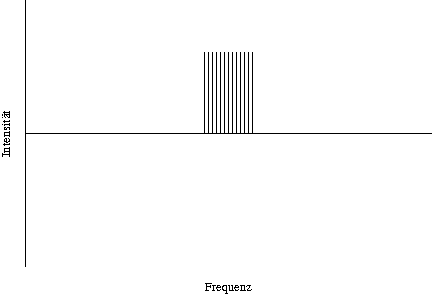
Greift man den strukturgebenden Gedanken wieder auf, setzt jedoch statt einem Frequenzspektrum bestehend aus zwei Frequenzen sehr viele Frequenzen ein, nimmt der Abstand zwischen den periodischen "Stummpunkten" immer mehr zu.

Vom ersten Beispiel beginnend ist die Frequenz also immer un­schär­fer und der Ort immer schärfer geworden. Die Schärfe des Orts kann man in diesem Diagramm daran erkennen, dass es viele Stellen gibt, an denen die Amplitude "klein" ist, die Wahrscheinlichkeit, dass sich an dieser Stelle also das Elektron manifestiert, ebenfalls klein ist.

Zur Erinnerung: Wäre das Elektron vollständig delokalisiert, wäre die Manifestationswahrscheinlichkeit überall gleich groß.

0.0.1.1.4 ↑ Vollständige Lokalisierung

Mathematisch kann man dieses Verfahren fortsetzen und grenzwertig Sinusfunktionen unendlich vieler Frequenzen überlagern. Das Ergebnis ist dann ein Signal, dass nur an genau einer Stelle auftritt. An allen anderen Stellen ist es Null.

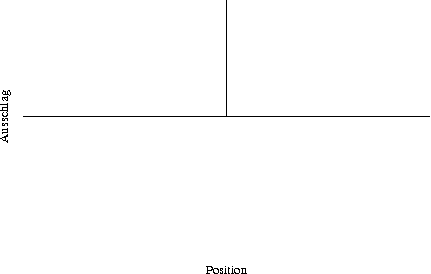
Dem entspricht eine vollständige Lokalisierung: Der Ort ist maximal scharf (Unschärfe Null), die Frequenz ist maximal unscharf (Unschärfe unendlich).

\underbrace{\Delta f}_{\infty \,\mathrm{Hz}} \cdot \underbrace{\Delta t}_{0 \,\mathrm{s}} \geq c;$\underset{\infty \text{Hz}}{\underbrace{\Delta f}}\cdot \underset{0\text{s}}{\underbrace{\Delta t}}\ge c;$

\underbrace{\Delta p}_{\infty \,\mathrm{Ns}} \cdot \underbrace{\Delta x}_{0 \,\mathrm{m}} \geq c;$\underset{\infty \text{Ns}}{\underbrace{\Delta p}}\cdot \underset{0\text{m}}{\underbrace{\Delta x}}\ge c;$

Über ein Elektron mit dieser Wellenfunktion könnte man genau sagen, wo es sich manifestieren wird. Es ist aber nicht möglich, seinen Impuls (und damit seine Geschwindigkeit) anzugeben. Es ist nichteinmal möglich, einige mögliche Werte des Impulses von anderen zu differenzieren – alle haben die gleiche Wahrscheinlichkeit.

0.0.1.2 ↑ Unschärferelation beim Doppelspalt

Senden wir eine Elektronenwelle auf einen Doppelspalt, lässt sich die "Bewegung" in zwei Abschnitte gliedern: den, vor dem Spalt, und den, nach dem Spalt.

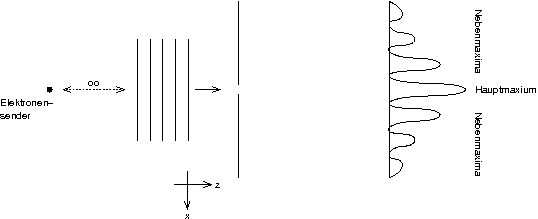
0.0.1.2.5 ↑ Elektronenwelle vor dem Spalt

Vor dem Spalt sind die eintreffenden Elektronen in z$z$-Richtung delokalisiert; die Elektronengeschwindigkeit, und damit der Impuls, ist (idealisiert) exakt bekannt.

Auch in x$x$-Richtung ist das Elektronium delokalisiert – der x$x$-Impuls ist exakt Null.

0.0.1.2.6 ↑ Elektronenwelle nach dem Spalt

Der Teil der Welle, der den Doppelspalt durchlaufen konnte, ist weiterhin in z$z$-Richtung delokalisiert, da sich die Elektronenwellengeschwindigkeit in z$z$-Richtung nicht geändert hat (und da insbesondere ihre Unschärfe konstant geblieben ist). (Natürlich ist bei einem realen Doppelspaltexperiment der Ort nicht vollständig delokalisiert, da er wohl kaum über den Versuchsaufbau hinausragt. Idealisiert nehmen wir daher an, dass Spalt und Schirm unendlich ausgedehnt sind.)

Der x$x$-Impuls hingegen ist nach dem Spalt unscharf – schließlich wird auf dem Schirm ein Interferenzmuster erzeugt, es manifestieren sich ja pro Messfläche, der Verteilung der Maxima entsprechend, unterschiedlich viele Elektronen pro Zeiteinheit.

Die Impulserhaltung wird dabei nicht verletzt, da die Ma­ni­fes­ta­tions­wahr­schein­lich­keit–x$x$-Kurve achsensymmetrisch ist. Bildlich gesprochen gibt es zu jedem Elektron, das sich unten manifestiert, eins, das sich entsprechend oben manifestiert.

Die Impulserhaltung ist sogar dann nicht verletzt, wenn man die "Elektronen" einzeln durch den Doppelspalt schickt: Dann tritt näm­lich der Festkörper als Impulsaustauschpartner auf.

(Beim Doppelspaltexperiment deswegen davon zu sprechen, dass sich Elektronen am Spalt stoßen und daher abgelenkt werden, ist aber natürlich nur solange zulässig, solange man selbst (und alle anderen am Gespräch Beteiligten) wissen, was eigentlich gemeinst ist; "man darf beliebig schlampig sprechen", solange der Sinn allen klar ist.)

0.0.1.3 ↑ Fragen

0.0.1.3.7 ↑ Nullpunkte eine Besonderheit?

Inwiefern unterscheiden sich die "Stummpunkte" der Schwebungszustände von den normalen Nullpunkten, die während jeder voll­stän­di­gen Periode zweimal auftreten?

Die einen scheinen strukturgebend zu sein, während die anderen keine physikalischen Konsequenzen haben.

0.0.1.3.7.2 ↑ Mögliche Lösung

Man wird wohl eine Funktion definieren müssen, die jedem x$x$-Wert den Wert der "theoretisch erreichbaren" Amplitude zuordnet, vergleichbar mit einer Einhüllenden:

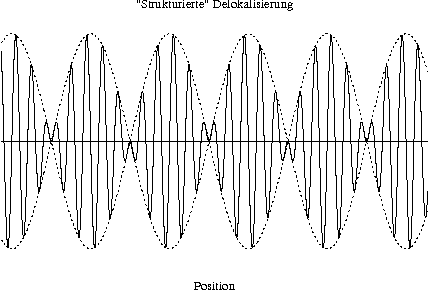
Dann interpretiert man nicht den Wert der eigentlichen Funktion als Maß für die Manifestationswahrscheinlichkeit, sondern den Wert der begrenzenden/einhüllenden Funktion.

Diese mögliche Lösung scheint mit allen angesprochenen Fällen konsistent zu sein; aber eine Rechtfertigung, wieso die restlichen, nicht-"Stummpunkt"-Nullstellen nicht relevant sind, ist sie sicherlich nicht.

0.0.1.3.8 ↑ Wechsel des Impulsaustauschpartners – qualitativer Unter­schied?

Treffen viele Elektronen pro Sekunde auf den Doppelspalt, ist die Impulserhaltung dadurch erfüllt, dass sich – bildlich gesprochen – "je ein Elektron oben und je ein Elektron unten manifestiert".

Treffen die Elektronen "einzeln" auf den Spalt, so ist dagegen der Festkörper Impulsaustauschpartner.

Nun gibt es ja aber zwischen diesen beiden Szenarien nur einen quantitativen, keinen qualitativen, Unterschied: Im ersten Fall treffen viele hundertausend Elektronen pro Sekunde, im zweiten nur einige zehn pro Sekunde auf den Spalt.

Aber der Impulsaustauschpartner ändert sich qualitativ! Im ersten Fall sind es andere Elektronen, im zweiten Fall der Festkörper.

0.0.1.3.8.3 ↑ Mögliche Lösungen

a)

Als Lösung wäre denkbar, dass – stochastisch verteilt – andere Elektronen und der Festkörper Impulsaustauschpartner sind. Die Wahrscheinlichkeit, dass der Festkörper Partner ist, ist dann im zweiten Fall sehr groß, während sie im ersten Fall sehr klein ist.

Damit hätte die quantitative Änderung der Anzahl der Elektronen pro Sekunde auch eine quantitative Konsequenz, nämlich die Änderung der Wahrscheinlichkeit, mit dem Festkörper Impuls auszutauschen anstatt mit anderen Elektronen.

b)

Alternativ wäre denkbar, dass der Impulserhaltungssatz nicht für jedes Elementarereignis gilt/angewendet werden kann/be­trach­tet werden darf, sondern dass er nur durchschnittlich gilt: E(\Delta p) = 0 \,\mathrm{Ns};$E\left(\Delta p\right)=0\text{Ns};$

0.0.1.3.9 ↑ Ortsunschärfe nach dem Spalt?

Da ja nach dem Spalt der Elektronenimpuls unscharf ist, kann die Ortsunschärfe abnehmen; die Unschärferelation würde dabei nicht verletzt werden. (Es besteht aber kein Zwang, dass die Ortsunschärfe abnimmt – es heißt ja \Delta x \Delta p > c$\Delta x\Delta p>c$, nicht \Delta x \Delta p = c$\Delta x\Delta p=c$.)

Nimmt die Ortsunschärfe tatsächlich ab? Wenn ja, inwiefern?

0.0.1.3.10 ↑ Negative Frequenzen? [FORMAL]

Bei einer grenzwertig unendlichen Frequenzunschärfe mit Erwartungswert \hat f$\widehat{f}$ müssten ja im Spektrum auch negative Frequenzen vorkommen. Ist das nicht problematisch, da Frequenzen ja immer positiv (oder zumindest nichtnegativ) sein müssen?

0.0.1.3.11 ↑ Übliche Bezeichnung für die "Stummpunkte"? [FORMAL]

Was ist die übliche Bezeichnung für die x$x$-Werte, die ich "Stummpunkte" genannt habe? (Die Bezeichnung "Stummpunkt" hat den Nachteil, dass sie begrifflich mit Tönen bzw. Schallwellen verbunden ist. Die Bezeichnung schließt also eine allgemeinere Verwendung aus.)