«K12/K13» 53. Hausaufgabe «PDF», «POD»

0.0.1 ↑ 53. Hausaufgabe

0.0.1.1 ↑ Exzerpt von B. S. 266: Energieübertragung im Wechselstromkreis und Vergleich mit unserer Herleitung

Der grundlegende Unterschied zwischen unserer Herleitung und der im Metzler ist der, dass wir keine Angst vorm Integral haben und einen Ansatz über die Energie wählten, während man im Metzler den Bereich der Leistung nicht verlässt:

\displaystyle E = \int\limits_{t_1}^{t_2} U(t) \, I(t) \,\mathrm{d}t;$E=\underset{t_1}{\overset{t_2}{\int \; <!--nolimits-->}}U\left(t\right)I\left(t\right)\text{d}t;$

Im Metzler dagegen finden wir

\displaystyle p = u \, i;$p=ui;$

Dies liegt vermutlich darin begründet, dass man die Leistung (wie z.B. auch die Stromstärke) leichter messen kann als die Energie (bzw. die Ladung). Wir nahmen also einen theoretischeren Ansatz, während im Metzler eine praxisorientierterer Ansatz zu finden ist.

Dementsprechend unterscheidet sich auch das weitere Vorgehen in der Herleitung: Sowohl unsere Herleitung als auch die im Metzler nutzt die Beziehungen U(t) = U_0 \sin \omega t$U\left(t\right)=U_{0}sin\omega t$ und I(t) = I_0 \sin \omega t$I\left(t\right)=I_{0}sin\omega t$ aus. Jedoch konnten wir, weil wir den Weg übers Integral gewählt haben, sehr anschaulich fortfahren:

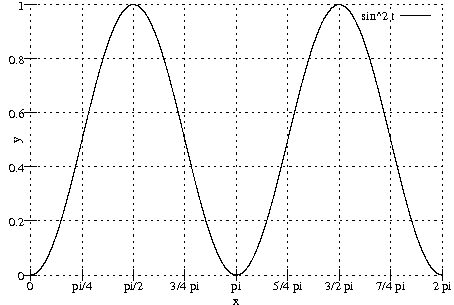
Dies ist – abzüglich der Konstanten U_0$U_0$ und I_0$I_0$ – der Graph der Funktion, die wir integrieren. "Klappt" man jeweils einen Teil des Graphen "um", so erkennt man, dass der Flächeninhalt der Fläche, die von der x$x$-Achse und dem Funktionsgraphen begrenzt wird, \frac{T}{2}$\frac{T}{2}$ beträgt:

\displaystyle \int\limits_{0 \,\mathrm{s}}^T U(t) I(t) \,\mathrm{d}t \stackrel{\scriptsize\text{z.B.}}{=} U_{\text{max}} I_{\text{max}} \underbrace{\int\limits_{0 \,\mathrm{s}}^T \sin^2 \omega t \,\mathrm{d}t}_{\frac{T}{2}} = \underbrace{U_{\text{max}} I_{\text{max}} T}_{\text{bekannt als "`}UIt\text{"'}} \cdot \frac{1}{2};$\underset{0\text{s}}{\overset{T}{\int \; <!--nolimits-->}}U\left(t\right)I\left(t\right)\text{d}t\stackrel{\text{z.B.}}{=}{U}_{\text{max}}{I}_{\text{max}}\underset{\frac{T}{2}}{\underbrace{\underset{0\text{s}}{\overset{T}{\int \; <!--nolimits-->}}{sin}^2\omega t\text{d}t}}=\underset{\text{bekannt als ”‘}UIt\text{”’}}{\underbrace{U_{\text{max}}{I}_{\text{max}}T}}\cdot \frac{1}{2};$

In der Herleitung im Metzlers dagegen wird mit der undurchsichtigeren Beziehung 2 \sin^2 \omega t = 1 + \cos 2 \omega t$2{sin}^2\omega t=1+cos2\omega t$ argumentiert.

Der letzte Teil der Herleitung – das Definieren von U_{\text{eff}}$U_{\text{eff}}$ und I_{\text{eff}}$I_{\text{eff}}$ ist den beiden Herleitungen gemeinsam; die beiden neuen Variablen werden mittels Substitution eingeführt:

\displaystyle \Delta E_T = \underbrace{U_{\text{max}} I_{\text{max}} T}_{\text{bekannt als "`}UIt\text{"'}} \cdot \frac{1}{2} = \frac{U_{\text{max}}}{\sqrt{2}} \frac{I_{\text{max}}}{\sqrt{2}} T \stackrel{\text{!}}{\equiv} U_{\text{eff}} \, I_{\text{eff}} \, T;$\Delta E_T=\underset{\text{bekannt als ”‘}UIt\text{”’}}{\underbrace{U_{\text{max}}{I}_{\text{max}}T}}\cdot \frac{1}{2}=\frac{U_{\text{max}}}{\sqrt{2}}\frac{I_{\text{max}}}{\sqrt{2}}T\stackrel{\text{!}}{\equiv }{U}_{\text{eff}}{I}_{\text{eff}}T;$

Persönlich bevorzuge ich unsere Herleitung, da die Zusammenhänge zwischen Energie, Spannung und Stromstärke durchs Integral sehr deutlich werden und da man unsere Herleitung auch auf andere Wechselstromarten als den sinusförmigen Wechselstrom übertragen kann – es muss lediglich das Integral anders aufgelöst werden. Außerdem empfand ich unsere Auflösung des Integrals viel anschaulicher als das Ausnutzen der trigonometrischen Beziehung 2 \sin^2 \omega t = 1 + \cos 2 \omega t$2{sin}^2\omega t=1+cos2\omega t$ im Metzler.

(Benötigte Zeit: 43 min + 4 min)