«K12/K13» 80. Hausaufgabe «PDF», «POD»

0.0.1 ↑ 80. Hausaufgabe

0.0.1.1 ↑ Kohärenz

Kohärenz ist eine kontinuierliche Eigenschaft von interferierenden Wellen; es gibt Wellen, die vollständig kohärent sind, welche, die vollständig inkohärent sind, und Wellen, die weder vollständig kohärent noch vollständig inkohärent sind.

Kohärenz definiert man üblicherweise über die Intensität der Ü­ber­la­ge­rung aller interferierenden Wellen [2]:

v = \frac{I_{\text{max}} - I_{\text{min}}}{I_{\text{max}} + I_{\text{min}}};$v=\frac{I_{\text{max}}-I_{\text{min}}}{I_{\text{max}}+I_{\text{min}}};$

Beispiel: Interferiert eine ideale Sinuswelle mit einer zeitverzögerten Kopie von sich selbst (technisch realisierbar durch halb­durch­läs­si­ge Spiegel, wie beispielsweise beim Michelsoninterferometer), so ist v = 1$v=1$:

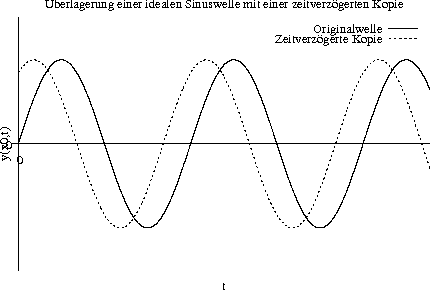
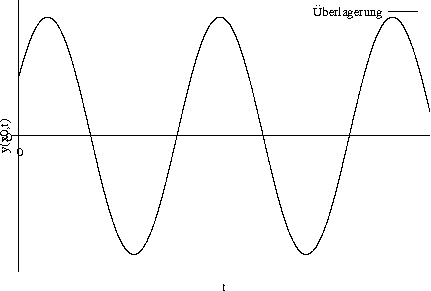
Der minimale Ausschlag ist 0 \,\frac{\mathrm{V}}{\mathrm{m}}$0\frac{\text{V}}{\text{m}}$, der maximale \hat A$Â$. Die Intensität ist direkt proportional zum Quadrat des Ausschlags; da wir die vollständige Formel für I$I$ nicht kennen (und diese für uns auch nicht interessant ist), fassen wir alle Konstanten, die wir nicht weiter berücksichtigen wollen, als k$k$ zusammen. Damit ist die Kohärenz dieses Szenarios:

v = \frac{I_{\text{max}} - I_{\text{min}}}{I_{\text{max}} + I_{\text{min}}} = \frac{k \hat A^2 - 0 \,\frac{\mathrm{V}}{\mathrm{m}}}{k \hat A^2 + 0 \,\frac{\mathrm{V}}{\mathrm{m}}} = \frac{k \hat A^2}{k \hat A^2} = 1;$v=\frac{I_{\text{max}}-I_{\text{min}}}{I_{\text{max}}+I_{\text{min}}}=\frac{k{Â}^2-0\frac{\text{V}}{\text{m}}}{k{Â}^2+0\frac{\text{V}}{\text{m}}}=\frac{k{Â}^2}{k{Â}^2}=1;$

Überlagert eine ideale Sinuswelle eine zeitverzögerte Kopie von ihr selbst, ist v = 1$v=1$; ideale Sinuswellen sind vollständig ko­hä­rent.

Bemerkbar macht sich das dadurch, dass Interferenzmuster der Überlagerung – beispielsweise am Schirm eines Michelsoninterferometers – sehr gut sichtbar sind. Interferieren dagegen zwei Wellen mit v < 1$v<1$, so ist die Sichtbarkeit (die Schärfe, der Kontrast) weniger gut.

Kohärenz ist also auch ein Maß für die Ausgeprägtheit des Interferenzmusters. In der Tat wird diese Eigenschaft oft auch als Definition der Kohärenz genutzt.

Man bezeichnet eine Welle als inkohärent, wenn v$v$ kleiner als ein bestimmter, zuvor ausgemachter Wert ist. Übliche Schwellenwerte sind 66 \,\%$66\%$, 50 \,\%$50\%$ und \frac{1}{e}$\frac{1}{e}$.

Den maximalen Weglängenunterschied, den zwei Lichtwellen, die einer gemeinsamen Quelle entstammen, haben dürfen, damit noch ein sichtbares Interferenzmuster entsteht, bezeichnet man als Ko­hä­renz­län­ge l_c$l_c$. Über \frac{l_c}{c} = t_c$\frac{l_c}{c}=t_c$ kann man die Kohärenzlänge in die Kohärenzzeit umrechnen.

Die Kohärenzzeit und -länge idealer Sinuswellen ist "unendlich"; ideale Sinuswellen sind immer vollständig kohärent. Sonnenlicht hat eine Kohärenzlänge von etwa einem Mikrometer [13]. Die Kohärenzlängen von Lasern liegen im Bereich einiger Zentimeter bis sogar mehreren Kilometern [14].

0.0.1.2 ↑ Michelsoninterferometer

Die wichtigsten grundlegenden Gesetze und Tatsachen der Physik sind entdeckt [...] und daher ist die Wahrscheinlichkeit, dass sie jemand durch neue Entdeckungen ergänzt, äußerst gering.

– Albert Abraham Michelson, 1903 [5]

Eine Möglichkeit der Bestimmung der Kohärenz eines Wellenfelds geht auf Albert Abraham Michelson zurück, den ersten amerikanischen Physiknobelpreisträger, der sich von 1887 bis etwa 1920 mit Interferometrie beschäftigte. Bekannt ist er für sein Michelsoninterferometer und den oben gedruckten Ausspruch [3].

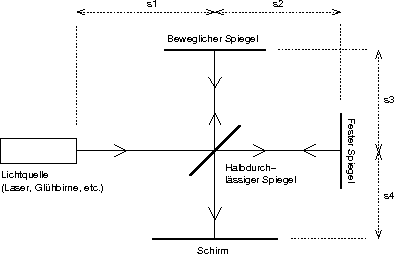
Beim Michelsoninterferometer wird eine eingehende Lichtwelle zuerst durch einen Strahlteiler, üblicherweise einem halb­durch­läs­si­gen Spiegel, in zwei Wellen geteilt. Der durchgelassene Teil der Welle wandert zum festen Spiegel rechts, zurück zum Strahlteiler und schließlich zum Schirm.

Der reflektierte Teil der Welle wandert zum beweglichen Spiegel oben, zurück zum Strahlteiler und schließlich ebenfalls zum Schirm, wo transmittierte und reflektierte Teilwelle interferieren [4].

Das Interferenzmuster hängt von den Phasen der beiden Teilwellen ab am Schirm ab. Hat eine der beiden Teilwellen beispielsweise gerade ein Maximum und die andere ein Minimum, so löschen sich beide vollständig aus; man spricht von vollständiger destruktiver Interferenz. Sind die Ausschläge der beiden Teilwellen beim Eintreffen auf dem Schirm beide maximal, kommt es zu vollständiger konstruktiver Interferenz.

Zur Bestimmung der Kohärenz der einfallenden Welle ist die Weg­län­gen­dif­fe­renz \Delta s$\Delta s$ interessant. Diese errechnet sich durch die Differenz der Längen, die die beiden Teilwellen zurücklegen, bis sie auf dem Schirm eintreffen.

\Delta s = \underbrace{\left(s_1 + s_2 + s_2 + s_4\right)}_{\text{Transmittierte Welle}} - \underbrace{\left(s_1 + s_3 + s_3 + s_4\right)}_{\text{Reflektierte Welle}} = 2 s_2 - 2 s_3;$\Delta s=\underset{\text{Transmittierte Welle}}{\underbrace{\left(s_1+s_2+s_2+s_4\right)}}-\underset{\text{Reflektierte Welle}}{\underbrace{\left(s_1+s_3+s_3+s_4\right)}}=2s_2-2s_3;$

Es stellt sich nun heraus, dass sich ein klar sichtbares Interferenzmuster nur dann herausbildet, wenn die Weglängendifferenz \Delta s$\Delta s$ kleinergleich als die Kohärenzlänge l_c$l_c$ ist: \Delta s \leq l_c;$\Delta s\le l_c;$

Ist \Delta s > l_c$\Delta s>l_c$, wird das sichtbare Interferenzmuster unscharf. Ist die Weglängendifferenz sehr viel größer als die Kohärenzlänge, so bildet sich fast gar kein sichtbares Muster mehr aus.

Variiert man s_3$s_3$, verschiebt man also den beweglichen Spiegel, ändert sich also die Sichtbarkeit des Interferenzmuster. Ändert man s_3$s_3$ so, dass das Interferenzmuster gerade noch sehr scharf ist, ist der Weglängenunterschied näherungsweise gleich der Kohärenzlänge.

Die wiederholte Verwendung des einschränkenden Adjektivs "sichtbar" in den vorhergehenden Absätzen hat einen Grund: Streng genommen bilden sich nämlich immer Interferenzmuster aus – schließlich interferieren die beiden Teilwellen immer, es gibt ja auch keinen Grund, wieso sie es nicht tun sollten.

Allerdings ändert sich das Muster zeitlich sehr schnell, wenn die Weglängendifferenz sehr viel größer als die Kohärenzlänge ist – mal interferieren die Wellen konstruktiv, dann destruktiv, dann wieder konstruktiv. Im Mittel wird weder destruktive noch konstruktive Interferenz bevorzugt; für unsere Augen entsteht dann nicht der Eindruck eines Musters, sondern nur der einer beleuchteten Fläche.

Es ist nicht so, als dass sich zwei Wellenzüge gegenseitig "beschnuppern" würden, und dann, je nachdem ob die beiden Wellenzüge genügend kohärent sind oder nicht, interferieren.

0.0.1.3 ↑ Zeitliche Kohärenz

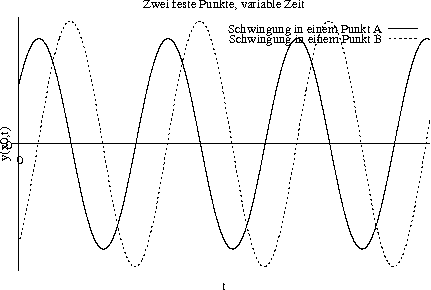
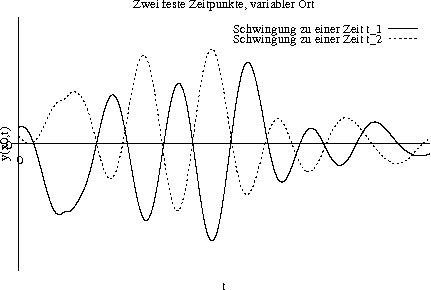
Ein Wellenfeld ist genau dann zeitlich kohärent, wenn die Phasendifferenz zwischen dem Signal der überlagerten Gesamtwelle in einem festen Punkt gegenüber einem anderen festen Punkt zu jeder Zeit gleich ist.

Anders ausgedrückt ist zeitliche Kohärenz ein Maß für die Einfarbigkeit eines Wellenfelds.

Beispiele:

• In einer Wellenwanne befinden sich an zwei unterschiedlichen, aber festen Orten je ein Korken, welche sich mit den Wellen in der Wellenwanne bewegen. Nun werden gerade Wellen gleicher Frequenz (\omega$\omega$ konst.) und gleicher Wellenausbreitungsrichtung (\vec k$\overrightarrow{k}$ konst.) erzeugt.

  
  

  Betrachtet man nun die Bewegung der Korken, so wird man beispielsweise feststellen, dass beide immer zugleich nach oben schwingen, dass beide immer zugleich das Schwingungsmaximum erreichen, dass beide immer zugleich nach unten schwingen usw. (Phasendifferenz 0^\circ$0^{\circ }$). Die Wellen sind in diesem Fall zeitlich kohärent.

  Es ist aber auch möglich, dass, immer dann, wenn der eine Korken sein Maximum erreicht hat, der andere Korken sein Minimum erreicht hat und umgekehrt (Phasendifferenz 180^\circ$180^{\circ }$). Auch in diesem Fall würde man von zeitlicher Kohärenz sprechen. Und auch die Fälle mit anderen Phasendifferenzen würde man der zeitlichen Kohärenz zuordnen.

  Man spricht nur dann nicht von zeitlicher Kohärenz, wenn sich die Phasendifferenz mit der Zeit ändert, also beispielsweise wenn zu einem Zeitpunkt beide Korken ihr Maximum erreicht haben, und zu einem anderen nur einer der beiden sein Maximum erreicht hat.

• In einer Wellenwanne werden mehrere gerade Wellen gleicher Frequenz (\omega$\omega$ konst.), aber unterschiedlicher Ausbreitungsrichtung (\vec k$\overrightarrow{k}$ nicht konstant) erzeugt. Auch hier wird man wieder feststellen, dass die Phasendifferenz der Schwingungen in zwei festen Punkten zeitlich unveränderlich ist; auch dieser Fall ist also zeitlich kohärent.

  
  

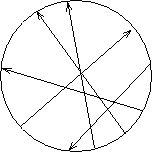
• Erzeugt man mehrere Wellen unterschiedlicher Frequenz, so ist die Phasendifferenz zwischen zwei Orten zeitlich nicht konstant, die Wellen sind also zeitlich inkohärent.

  
  

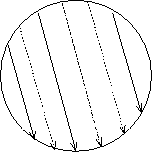
0.0.1.4 ↑ Räumliche Kohärenz

Ein Wellenfeld ist genau dann räumlich kohärent, wenn die Phasendifferenz zwischen dem Signal der überlagerten Gesamtwelle zu einem festen Zeitpunkt gegenüber einem anderen festen Zeitpunkt in jedem Ort gleich ist.

Anders ausgedrückt ist zeitliche Kohärenz ein Maß für die "Geradheit" bzw. "Ebenheit" eines Wellenfelds.

Beispiele:

• Mehrere ebene Wellen der gleichen Frequenz (\omega$\omega$ konst.) sind räumlich kohärent. Die Richtung der Wellen spielt dabei keine Rolle.

  
  

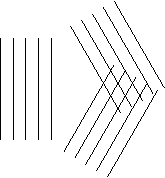
• Sogar mehrere gerade Wellen unterschiedlicher Frequenz (\omega$\omega$ nicht konstant) sind räumlich kohärent [Achtung, widerspricht Unterricht, entspricht aber mehreren Quellen [6], [7], [8], [9], [10], [11], [12]]:

  
  

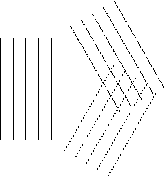
• Mehrere punktförmige Wellen sind räumlich inkohärent. Die Frequenz der Wellen spielt keine Rolle [Achtung, widerspricht Unterricht, entspricht aber mehreren Quellen [6], [7], [8], [9], [10], [11], [12]]:

  
  

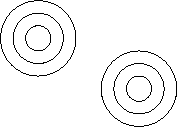
0.0.1.5 ↑ Intensität

Intensität kennen wir flüchtig bereits unter einem anderen Begriff, Energiestrom pro Fläche. Die Einheit der Intensität ist \left[\frac{\mathrm{J}}{\mathrm{s} \cdot \mathrm{m}^2}\right]$\left[\frac{\text{J}}{\text{s}\cdot {\text{m}}^2}\right]$.

Intensitäten kann man immer angeben, wenn Energie fließt. Für uns besonders interessant ist Intensität aber im Kontext von (elektromagnetischen) Wellen.

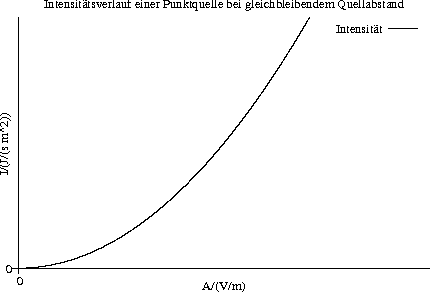
• Intensität ist indirekt proportional zum Quadrat der Entfernung von der Lichtquelle [1].

  I \sim \frac{1}{r^2};$I\sim \frac{1}{r^2};$

  Grund: Summiert (integriert) man die Intensitäten von jedem Punkt einer Hüllfläche um die Lichtquelle auf, so erhält man den gesamten Energiestrom (die Gesamtleistung).

  Im einfachen Fall der kugelförmigen Hüllfläche mit Radius r$r$ können wir das Integral auflösen:

  I_E = P = I(r) \, 4 \pi r^2;$I_E=P=I\left(r\right)4\pi r^2;$

  Aufgelöst nach I(r)$I\left(r\right)$ erhält man für die Intensität im Abstand r$r$ von der Punktquelle:

  I(r) = \frac{P}{4 \pi r^2};$I\left(r\right)=\frac{P}{4\pi r^2};$

  

• Außerdem ist die Intensität direkt proportional zum Quadrat der Amplitude der Überlagerungswelle:

  I \sim A_{\text{ges}}^2;$I\sim A_{\text{ges}}^2;$

  

0.0.1.6 ↑ Herleitung der Gleichung für ebene Wellen

Möchte man verschiedene Szenarien mittels Graphenplotter visualisieren, muss man natürlich die Gleichung für ebene Wellen kennen. Die Gleichung für Kreiswellen ist einfach –

f(x,y,t) = A \sin 2\pi\left(f t + \frac{1}{\lambda} r\right) = A \sin 2\pi\left(f t + \frac{1}{\lambda} \sqrt{\left(x - x_{\text{Quelle}}\right)^2 + \left(y - y_{\text{Quelle}}\right)^2}\right)\!;$f\left(x,y,t\right)=Asin2\pi \left(ft+\frac{1}{\lambda }r\right)=Asin2\pi \left(ft+\frac{1}{\lambda }\sqrt{{\left(x-x_{\text{Quelle}}\right)}^2+{\left(y-y_{\text{Quelle}}\right)}^2}\right);$

Bei Kreiswellen ist die Entfernung von einem bestimmten Wellenpunkt (x,y)$\left(x,y\right)$ zur punktförmigen Quelle (x_{\text{Quelle}},y_{\text{Quelle}})$\left(x_{\text{Quelle}},y_{\text{Quelle}}\right)$ wichtig. Bei geraden Wellen ist die Quelle idealisiert aber eine Gerade, kein einzelner Punkt. Entscheidend ist also die Entfernung von einem bestimmten Wellenpunkt (x,y)$\left(x,y\right)$ zur Quellgeraden (y_{\text{Quelle}} = m_{\text{Quelle}} x + t_{\text{Quelle}}$y_{\text{Quelle}}=m_{\text{Quelle}}x+t_{\text{Quelle}}$).

Das Problem dabei ist, eine Formel für den Abstand eines Punktes zu einer Geraden zu finden.

Um sie zu finden, legen wir ein Geradenbüschel durch den allgemeinen Punkt B(x_B, y_B)$B\left(x_B,y_B\right)$, und überprüfen dann, welche der Geraden des Büschels senkrecht zur Quellgeraden steht. Anschließend berechnen wir die Entfernung von B$B$ zum Schnittpunkt von Quellgerade und der Senkrechten.

y_Q = \tan\alpha x_Q + t_Q; \Leftrightarrow t_Q = y_Q - \tan\alpha x_Q;$y_Q=tan\alpha x_Q+t_Q;\iff t_Q=y_Q-tan\alpha x_Q;$ (Q$Q$ ist ein beliebiger Punkt auf der Quellgeraden.)

y_B = m x_B + t_B; \Leftrightarrow t_B = y_B - m x_B;$y_B=m{x}_B+t_B;\iff t_B=y_B-m{x}_B;$

m \cdot \tan\alpha = -1; \Leftrightarrow m = -\frac{1}{\tan\alpha};$m\cdot tan\alpha =-1;\iff m=-\frac{1}{tan\alpha };$ (Gesucht ist die Schargerade, die senkrecht zur Quellgeraden steht.)

y_\perp = -\frac{1}{\tan\alpha} x + y_B + \frac{1}{\tan\alpha} x_B;$y_{\perp }=-\frac{1}{tan\alpha }x+y_B+\frac{1}{tan\alpha }{x}_B;$ (Senkrechte zur Quellgeraden durch B$B$)

y_\perp y_{\text{Quelle}}; \Leftrightarrow -\frac{1}{\tan\alpha} x + y_B + \frac{1}{\tan\alpha} x_B = \tan\alpha x + y_Q - \tan\alpha x_Q;$y_{\perp }{y}_{\text{Quelle}};\iff -\frac{1}{tan\alpha }x+y_B+\frac{1}{tan\alpha }{x}_B=tan\alpha x+y_Q-tan\alpha x_Q;$ (Schnittpunkt der Senkrechten mit der Quellgeraden)

x = \frac{y_B + x_B \frac{1}{\tan\alpha} - y_Q + x_Q \tan\alpha}{\tan\alpha + \frac{1}{\tan\alpha}};$x=\frac{y_B+x_B\frac{1}{tan\alpha }-y_Q+x_{Q}tan\alpha }{tan\alpha +\frac{1}{tan\alpha }};$

Setzt man dieses x$x$ in die Geradengleichung der Quellgeraden ein, so erhält man die y$y$-Koordinate des Schnittpunkts. Mit bekannter x$x$- und y$y$-Koordinate kann man dann die Entfernung zur Quellgeraden wie gewohnt mittels dem Satz des Pythagoras bestimmen.

0.0.1.7 ↑ Abschließende Bemerkung

Viele Quellen über Kohärenz gehen sehr schnell auf technisch wichtige Details über Laser ein – welche Art von Laser, wie müssen Laser auf "optical tables" befestigt werden, wie können Er­schüt­te­run­gen am besten gedämpft werden, usw. –, erläutern die Bedeutung von Kohärenz im Rahmen der Quantenphysik (besonders auffällig war das Bose–Einstein-Kondensat), oder nutzen vektorielle Wellengleichungen und Fouriertransformationen, zu deren Interpretation wir noch nicht in der Lage sind.

Dies behindert natürlich den Lernprozess: Man möchte weniger über die genauen technisch relevanten Details bescheid wissen, sondern sich erst ein Gesamtbild machen. Später kann man sich dann mit Details auseinandersetzen.

Ein großes Problem war auch, dass es mir nicht möglich war, ein widerspruchsfreies Bild über Kohärenz herzuleiten, solange ich an der Korrektheit unserer Unterrichtsstunde über Kohärenz festhielt; alle Quellen, die ich erfolgreich interpretieren konnte, widersprachen dem Tafelbild.

Da die Quellen unter sich widerspruchsfrei waren, die Definitionen von zeitlicher und räumliche Kohärenz nach den Quellen (Phasendifferenz bei zwei festen Punkten und variabler Zeit bzw. zwei festen Zeitpunkten und variablen Ort) mir einleuchteten und die Graphen der Unterrichtsszenarien die Definitionen auch unterstützten, entschied ich mich mangels Alternativen, der Literatur zu folgen.

Wird Kohärenz wirklich so unterschiedlich verstanden?

0.0.1.8 ↑ Quellen

[1]

Wikipedia-Eintrag zu Intensität: http://de.wikipedia.org/wiki/Intensit%C3%A4t_%28Physik%29

[2]

Grundlagen von zeitlicher und räumlicher Kohärenz im Hinblick auf Laserphysik von Rico Poser: http://www.philippi-trust.de/hendrik/braunschweig/wirbeldoku/poser.html (unten)

[3]

Wikipedia-Eintrag zu Michelson: http://de.wikipedia.org/wiki/Albert_Abraham_Michelson

[4]

Nichtöffentliches Vorlesungsskript von Mark Wolf über Wellenoptik

[5]

Prognosen und Thesen ... nicht nur zum Schmunzeln von Hermann Maurer, veröffentlicht im Informatik-Spektrum 23 (2000) 1, S. 51–59

[6]

Englischer Wikipedia-Eintrag zu Kohärenz: http://en.wikipedia.org/wiki/Coherence_%28physics%29

[7]

Mail von Kai-Martin Knaak über räumliche Kohärenz: http://groups.google.com/group/de.sci.electronics/msg/24397da84162bfde

[8]

Lasers: What is Coherence? von William Beaty: http://amasci.com/miscon/coherenc.html

[9]

Wikipedia-Eintrag zu kohärenter Strahlung: http://de.wikipedia.org/wiki/Koh%C3%A4rente_Strahlung

[10]

Mail von "Billy Fish" über räumliche und zeitliche Kohärenz: http://groups.google.com/group/sci.optics/msg/1970bdc7f85af635?hl=en&

[11]

Mail von Gleb Vdovin über die Beziehung von räumlicher Kohärenz und der "Geradheit" von Wellen: http://groups.google.com/group/sci.optics/msg/fa3abc93119670d4?hl=en&

[12]

Mail von Doug Goncz über den Zusammenhang von räumlicher Kohärenz und Kreiswellen: http://groups.google.com/group/sci.physics/msg/59c39f04a67b5988?hl=en&

[13]

Skript über Wellenoptik von T. Hebbeker: http://www.physik.rwth-aachen.de/~hebbeker/lectures/ph3_0203/p323_l05/p323_l05.html

[14]

Englischer Wikipedia-Eintrag zur Kohärenzlänge: http://en.wikipedia.org/wiki/Coherence_length