«K12/K13» 18. Hausaufgabe «PDF», «POD»

0.0.1 ↑ 18. Hausaufgabe

0.0.1.1 ↑ Analysis-Buch Seite 70, Aufgabe 33

Gegeben sind die Funktionen

\mathrm{p}\colon x \mapsto \mathrm{p}(x) := -\frac{1}{2}\left(x - 3\right)^2 + \frac{9}{2}; \quad D_{\mathrm{p}} = \mathds{R};$\text{p}:x\mapsto \text{p}\left(x\right):=-\frac{1}{2}{\left(x-3\right)}^2+\frac{9}{2};D_{\text{p}}=\mathbb{ℝ};$

\mathrm{g}_a\colon x \mapsto \mathrm{g}_a(x) := ax; \quad D_{\mathrm{g}_a} = \mathds{R}; \quad a \in \mathds{R};${\text{g}}_a:x\mapsto {\text{g}}_a\left(x\right):=ax;D_{{\text{g}}_a}=\mathbb{ℝ};a\in \mathbb{ℝ};$

a)

Berechne den Inhalt A$A$ der Fläche, die von der Parabel und der x$x$-Achse eingeschlossen ist.

\mathrm{p}(x) = 0; \Rightarrow -\frac{1}{2}x^2 + 3x = 0;$\text{p}\left(x\right)=0;\Rightarrow -\frac{1}{2}{x}^2+3x=0;$

⇒ x_1 = 0; \quad -\frac{1}{2}x_2 = -3; \Rightarrow x_2 = 6;$x_1=0;-\frac{1}{2}{x}_2=-3;\Rightarrow x_2=6;$

⇒ \mathrm{p}(x) = -\frac{1}{2}x\left(x - 6\right);$\text{p}\left(x\right)=-\frac{1}{2}x\left(x-6\right);$

⇒ VZW von -$-$ nach +$+$ bei 0$0$ und von +$+$ nach -$-$ bei 6$6$;

⇒ A = \int\limits_0^6 \mathrm{p}(x) \,\mathrm{d}x = \left[-\frac{1}{6}x^3 + \frac{3}{2}x^2\right]_0^6 = 18;$A=\underset{0}{\overset{6}{\int \; <!--nolimits-->}}\text{p}\left(x\right)\text{d}x={\left[-\frac{1}{6}{x}^3+\frac{3}{2}{x}^2\right]}_0^6=18;$

b)

Berechne die Koordinaten der Punkte P$P$ und Q$Q$, in denen sich G_{\mathrm{p}}$G_{\text{p}}$ und G_{\mathrm{g}_a}$G_{{\text{g}}_a}$ schneiden.

\mathrm{p}(x) = \mathrm{g}_a(x); \Rightarrow -\frac{1}{2}x^2 + 3x = ax;$\text{p}\left(x\right)={\text{g}}_a\left(x\right);\Rightarrow -\frac{1}{2}{x}^2+3x=ax;$

⇒ x_3 = 0; \quad -\frac{1}{2}x_4^2 + \left(3 - a\right) = 0; \Rightarrow x_4 = 6 - 2a;$x_3=0;-\frac{1}{2}{x}_4^2+\left(3-a\right)=0;\Rightarrow x_4=6-2a;$

⇒ P(0,0); \quad Q(6-2a, 6a-2a^2);$P\left(0,0\right);Q\left(6-2a,6a-2a^2\right);$

c)

Berechne den Inhalt B(a)$B\left(a\right)$ der Fläche, die zwischen G_{\mathrm{p}}$G_{\text{p}}$ und G_{\mathrm{g}_a}$G_{{\text{g}}_a}$ liegt.

\renewcommand{\arraystretch}{2.0}\begin{array}{rcl} {} \mathrm{B}(a) &:=& \left| \int\limits_0^{6-2a} \mathrm{p}(x) \,\mathrm{d}x - \int\limits_0^{6-2a} \mathrm{g}_a(x) \,\mathrm{d}x \right| = \biggl| \left[-\frac{1}{6}x^3 + \frac{3}{2}x^2\right]_0^{6-2a} - \left[\frac{a}{2}x^2\right]_0^{6-2a} \biggr| = \\ {} && \left|-\frac{1}{6}\left(6-2a\right)^3 + \frac{3}{2}\left(6-2a\right)^2 - \frac{a}{2}\left(6-2a\right)^2\right| = \left(6-2a\right)^2 \left|-1 + \frac{1}{3}a + \frac{3}{2} - \frac{a}{2}\right| = \\ {} && \left| \frac{1}{12} \left(6-2a\right)^3 \right| = \frac{2}{3} \left|3-a\right|^3; \end{array}$\begin{array}{ccc}\hfill \text{B}\left(a\right)& \hfill :=\hfill & \left|\underset{0}{\overset{6-2a}{\int \; <!--nolimits-->}}\text{p}\left(x\right)\text{d}x-\underset{0}{\overset{6-2a}{\int \; <!--nolimits-->}}{\text{g}}_a\left(x\right)\text{d}x\right|=\mid {\left[-\frac{1}{6}{x}^3+\frac{3}{2}{x}^2\right]}_0^{6-2a}-{\left[\frac{a}{2}{x}^2\right]}_0^{6-2a}\mid =\hfill \\ \hfill & \hfill \hfill & \left|-\frac{1}{6}{\left(6-2a\right)}^3+\frac{3}{2}{\left(6-2a\right)}^2-\frac{a}{2}{\left(6-2a\right)}^2\right|={\left(6-2a\right)}^2\left|-1+\frac{1}{3}a+\frac{3}{2}-\frac{a}{2}\right|=\hfill \\ \hfill & \hfill \hfill & \left|\frac{1}{12}{\left(6-2a\right)}^3\right|=\frac{2}{3}{\left|3-a\right|}^3;\hfill \end{array}$

d)

Für welchen Wert von a$a$ liegt zwischen G_{\mathrm{p}}$G_{\text{p}}$ und G_{\mathrm{g}_a}$G_{{\text{g}}_a}$ keine Fläche? Welche besondere Lage hat dann G_{\mathrm{p}}$G_{\text{p}}$ zu G_{\mathrm{g}_a}$G_{{\text{g}}_a}$?

\mathrm{B}(a) = 0; \Rightarrow 3 - a = 0; \Rightarrow a = 3;$\text{B}\left(a\right)=0;\Rightarrow 3-a=0;\Rightarrow a=3;$

G_{\mathrm{g}_a}$G_{{\text{g}}_a}$ ist dann Tangente von G_{\mathrm{p}}$G_{\text{p}}$ an der Stelle 0$0$. (Beweis: \mathrm{g}_3'(0) = \mathrm{p}'(0);${\text{g}}_3^{\prime }\left(0\right)={\text{p}}^{\prime }\left(0\right);$)

e)

Eine Gerade durch den Ursprung geht durch den Scheitel der Parabel; diese Gerade zerlegt die Fläche A$A$ von a) in zwei Teilflächen. Berechne das Verlältnis: größere Teilfläche durch kleinere Teilfläche.

\mathrm{p}'(x_5) = 0; \Rightarrow x_5 = 3; \quad \mathrm{p}(3) = 9;${\text{p}}^{\prime }\left(x_5\right)=0;\Rightarrow x_5=3;\text{p}\left(3\right)=9;$

\mathrm{u}(x) := \frac{\mathrm{p}(3)}{6}x = \frac{3}{2}x;$\text{u}\left(x\right):=\frac{\text{p}\left(3\right)}{6}x=\frac{3}{2}x;$

⇒ \dfrac{A - \left(\int\limits_0^3 \mathrm{p}(x) \,\mathrm{d}x - \int\limits_0^3 \mathrm{u}(x) \,\mathrm{d}x\right)}{\int\limits_0^3 \mathrm{p}(x) \,\mathrm{d}x - \int\limits_0^3 \mathrm{u}(x) \,\mathrm{d}x} = \dfrac{A}{9 - \frac{27}{4}} - 1 = 7;$\frac{A-\left(\underset{0}{\overset{3}{\int \; <!--nolimits-->}}\text{p}\left(x\right)\text{d}x-\underset{0}{\overset{3}{\int \; <!--nolimits-->}}\text{u}\left(x\right)\text{d}x\right)}{\underset{0}{\overset{3}{\int \; <!--nolimits-->}}\text{p}\left(x\right)\text{d}x-\underset{0}{\overset{3}{\int \; <!--nolimits-->}}\text{u}\left(x\right)\text{d}x}=\frac{A}{9-\frac{27}{4}}-1=7;$

f)

Für welchen Wert von a$a$ ist \mathrm{B}(a)$\text{B}\left(a\right)$ achtmal so groß wie die Fläche zwischen der Parabel und der x$x$-Achse?

\mathrm{B}(a) = 8 A; \Rightarrow \frac{2}{3}\left|3 - a\right|^3 = 8 A; \Rightarrow \left(3 - a\right)^3 = \pm 12 A; \Rightarrow a = 3 - \sqrt[3]{\pm 12 A}$\text{B}\left(a\right)=8A;\Rightarrow \frac{2}{3}{\left|3-a\right|}^3=8A;\Rightarrow {\left(3-a\right)}^3=\pm 12A;\Rightarrow a=3-\sqrt[3]{\pm 12A}$ "=$=$" 3 - \sqrt[3]{\pm 216}$3-\sqrt[3]{\pm 216}$ "=$=$" 3 - \pm 2 \cdot 3; \Rightarrow a_1 = -3; \quad a_2 = 9;$3-\pm 2\cdot 3;\Rightarrow a_1=-3;a_2=9;$

g)

\int\limits_c^x \mathrm{p}(t) \,\mathrm{d}t =: \mathrm{I}_c(x);$\underset{c}{\overset{x}{\int \; <!--nolimits-->}}\text{p}\left(t\right)\text{d}t=:{\text{I}}_c\left(x\right);$

Berechne die Integralfunktion \mathrm{I}_c${\text{I}}_c$ von p$p$.

\mathrm{I}_c(x) = \int\limits_c^x \mathrm{p}(t) \,\mathrm{d}t = \left[-\frac{1}{6}x^3 + \frac{3}{2}x^2\right]_c^x = \frac{1}{6}\left(-x^3 + 9x^2 + c^3 - 9c^2\right);${\text{I}}_c\left(x\right)=\underset{c}{\overset{x}{\int \; <!--nolimits-->}}\text{p}\left(t\right)\text{d}t={\left[-\frac{1}{6}{x}^3+\frac{3}{2}{x}^2\right]}_c^x=\frac{1}{6}\left(-x^3+9x^2+c^3-9c^2\right);$

h)

Für welche Werte von c$c$ ist \mathrm{I}_c${\text{I}}_c$ symmetrisch zum Koordinatensystem?

\mathrm{I}_c(x) = \mathrm{I}_c(-x); \Rightarrow -1 = 0;${\text{I}}_c\left(x\right)={\text{I}}_c\left(-x\right);\Rightarrow -1=0;$

\mathrm{I}_c(x) = -\mathrm{I}_c(-x);${\text{I}}_c\left(x\right)=-{\text{I}}_c\left(-x\right);$ ⇒ (Keine von x$x$ unabhängige Aussage)

⇒ Es gibt kein c \in \mathds{R}$c\in \mathbb{ℝ}$, für welches \mathrm{I}_c${\text{I}}_c$ symmetrisch zum Koordinatensystem ist;

i)

Für welche Werte von c$c$ geht \mathrm{I}_c${\text{I}}_c$ durch den Ursprung?

\mathrm{I}_c(0) = 0; \Rightarrow -x^3 + 9x^2 + c^3 - 9c^2 = 0;${\text{I}}_c\left(0\right)=0;\Rightarrow -x^3+9x^2+c^3-9c^2=0;$

⇒ c_1 = 0; \quad c_2 - 9 = 0; \Rightarrow c_2 = 9;$c_1=0;c_2-9=0;\Rightarrow c_2=9;$

0.0.1.2 ↑ Analysis-Buch Seite 72, Aufgabe 61

\mathrm{f}_a(x) := -\frac{4}{a^2}\left(8 - a\right)\left(x^2 - ax\right); \quad D_{\mathrm{f}_a} = \mathds{R}; \quad a \neq 0;${\text{f}}_a\left(x\right):=-\frac{4}{a^2}\left(8-a\right)\left(x^2-ax\right);D_{{\text{f}}_a}=\mathbb{ℝ};a\ne 0;$

a)

Bestimme den Flächeninhalt \mathrm{A}(a)$\text{A}\left(a\right)$ der Fläche zwischen G_{\mathrm{f}_a}$G_{{\text{f}}_a}$ und der x$x$-Achse.

\mathrm{f}_a(x) = 0; \Rightarrow x^2 - ax = 0;${\text{f}}_a\left(x\right)=0;\Rightarrow x^2-ax=0;$

⇒ x_1 = 0; \quad x_2 - a = 0; \Rightarrow x_2 = a;$x_1=0;x_2-a=0;\Rightarrow x_2=a;$

⇒ \mathrm{f}_a(x) = -\frac{4}{a^2}\left(8 - a\right) \cdot x\left(x - a\right);${\text{f}}_a\left(x\right)=-\frac{4}{a^2}\left(8-a\right)\cdot x\left(x-a\right);$

\mathrm{A}(a) = \left|\int\limits_0^a \mathrm{f}_a(x) \,\mathrm{d}x\right| = \biggl|-\frac{4}{a^2}\left(8 - a\right)\left[\frac{x^3}{3} - \frac{a}{2}x^2\right]_0^a\biggr| = \dfrac{2}{3}\biggl|\left(8 - a\right) a\biggr|;$\text{A}\left(a\right)=\left|\underset{0}{\overset{a}{\int \; <!--nolimits-->}}{\text{f}}_a\left(x\right)\text{d}x\right|=\mid -\frac{4}{a^2}\left(8-a\right){\left[\frac{x^3}{3}-\frac{a}{2}{x}^2\right]}_0^a\mid =\frac{2}{3}\mid \left(8-a\right)a\mid ;$

b)

Für welche a$a$ ist der Inhalt der Fläche \mathrm{A}(a)$\text{A}\left(a\right)$ gleich 8$8$?

\mathrm{A}(a) = 8; \Rightarrow \frac{2}{3}\left(8 - a\right)a = \pm_1 8; \Rightarrow \left(8 - a\right)a = \pm_1 12; \Rightarrow -a^2 + 8a \mp_1 12 = 0;$\text{A}\left(a\right)=8;\Rightarrow \frac{2}{3}\left(8-a\right)a={\pm }_{1}8;\Rightarrow \left(8-a\right)a={\pm }_{1}12;\Rightarrow -a^2+8a{\mp }_{1}12=0;$

⇒ a_{1,2,3,4} = \dfrac{-8 \pm_2 \sqrt{64 + 4 \cdot \mp_1 12}}{-2} = \dfrac{-8 \pm_2 4\sqrt{4 \mp_1 3}}{-2} = 4 \mp_2 2\sqrt{4 \mp_1 3};$a_{1,2,3,4}=\frac{-8{\pm }_2\sqrt{64+4\cdot {\mp }_{1}12}}{-2}=\frac{-8{\pm }_{2}4\sqrt{4{\mp }_{1}3}}{-2}=4{\mp }_{2}2\sqrt{4{\mp }_{1}3};$

⇒ a_1 = 2; \quad a_2 = 6;$a_1=2;a_2=6;$ \\$$ ⇒ a_3 = 4 + 2\sqrt{7}; \quad a_4 = 4 - 2\sqrt{7};$a_3=4+2\sqrt{7};a_4=4-2\sqrt{7};$

(Kontrolle durch Einsetzen in Anfangsgleichung beweist Korrektheit.)

Es gibt aber kein globales Maximum, da \mathrm{A}(a) \to \infty$\text{A}\left(a\right)\to \infty$ für a \to \pm\infty$a\to \pm \infty$.

c)

Bestimme a$a$ so, dass \mathrm{A}(a)$\text{A}\left(a\right)$ möglichst groß wird. Gib den maximalen Flächeninhalt an.

\frac{\mathrm{d}}{\mathrm{d}a} \mathrm{A}(a) = \operatorname{sgn}\!\left(\frac{2}{3}\left(8-a\right)a\right) \cdot \frac{2}{3}\left(8 - 2a\right) = 0;$\frac{\text{d}}{\text{d}a}\text{A}\left(a\right)=sgn\left(\frac{2}{3}\left(8-a\right)a\right)\cdot \frac{2}{3}\left(8-2a\right)=0;$ (für a \neq 0$a\ne 0$)

⇒ 8 = 2a_5; \Rightarrow a_5 = 4;$8=2a_5;\Rightarrow a_5=4;$ (VZW gegeben)

\mathrm{A}(4) = \frac{32}{3};$\text{A}\left(4\right)=\frac{32}{3};$

d)

\mathrm{F}_4(x) := \int\limits_4^x \mathrm{f}_4(t) \,\mathrm{d}t;${\text{F}}_4\left(x\right):=\underset{4}{\overset{x}{\int \; <!--nolimits-->}}{\text{f}}_4\left(t\right)\text{d}t;$

Bestimme den Term \mathrm{F}_4(x)${\text{F}}_4\left(x\right)$ und alle Nullstellen von \mathrm{F}_4${\text{F}}_4$.

\mathrm{F}_4(x) = \int\limits_4^x \mathrm{f}_4(t) \,\mathrm{d}t\int\limits_4^x \mathrm{f}_4(t) \,\mathrm{d}t = -\frac{1}{3}x^3 + 2x^2 - \frac{32}{3};${\text{F}}_4\left(x\right)=\underset{4}{\overset{x}{\int \; <!--nolimits-->}}{\text{f}}_4\left(t\right)\text{d}t\underset{4}{\overset{x}{\int \; <!--nolimits-->}}{\text{f}}_4\left(t\right)\text{d}t=-\frac{1}{3}{x}^3+2x^2-\frac{32}{3};$

Nullstellen: \mathrm{F}_4(x) = 0; \Rightarrow x_3 = -2; \quad x_4 = 4;${\text{F}}_4\left(x\right)=0;\Rightarrow x_3=-2;x_4=4;$

e)

Berechne die Hoch-, Tief- und Wendepunkte von \mathrm{G}_{\mathrm{F}_4}${\text{G}}_{{\text{F}}_4}$.

\mathrm{f}_4(x) = -x\left(x - 4\right);${\text{f}}_4\left(x\right)=-x\left(x-4\right);$

⇒ VZW von \mathrm{f}_4${\text{f}}_4$ von -$-$ nach +$+$ bei 0$0$ und von +$+$ nach -$-$ bei a$a$;

⇒ P_{\text{HOP}}(4, 0);$P_{\text{HOP}}\left(4,0\right);$

⇒ P_{\text{TEP}}\!\left(0, -\frac{32}{3}\right);$P_{\text{TEP}}\left(0,-\frac{32}{3}\right);$

\mathrm{f}_4'(x) = 4 - 2x = -2 \left(x - 2\right);${\text{f}}_4^{\prime }\left(x\right)=4-2x=-2\left(x-2\right);$

⇒ VZW von \mathrm{f}_4'${\text{f}}_4^{\prime }$ von +$+$ nach -$-$ bei 2$2$;

⇒ P_{\text{WEP}}\!\left(2, -\frac{16}{3}\right);$P_{\text{WEP}}\left(2,-\frac{16}{3}\right);$

f)

Skizziere G_{\mathrm{f}_4}$G_{{\text{f}}_4}$ und G_{\mathrm{F}_4}$G_{{\text{F}}_4}$ in ein und demselben Koordinatensystem.

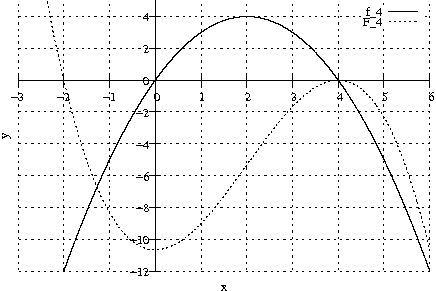
"Und das kann man zweimal unterstreichen, wenn das einen befriedigt"

"[Jeder ist] defizitär"

"Mei' Doofheit hat halt keine Grenzen"