«11C» Kreisbewegung «PDF», «POD»

0.0.1 ↑ Kreisbewegung

Bogenlänge: s = \varphi \cdot r;$s=\varphi \cdot r;$

Mittlere Geschwindigkeit: \overline{v} = \frac{\Delta x}{\Delta t};$\overline{v}=\frac{\Delta x}{\Delta t};$

Mittlere Winkelgeschwindigkeit: \overline{\omega} = \frac{\Delta \varphi}{\Delta t}; \quad \left[\overline{\omega}\right] = \frac{1}{\mathrm{s}};$\overline{\omega }=\frac{\Delta \varphi }{\Delta t};\left[\overline{\omega }\right]=\frac{1}{\text{s}};$

Konstante Winkelgeschwindigkeit: \omega = \frac{\Delta \varphi}{\Delta t} = \frac{\varphi - \varphi_0}{t - t_0};$\omega =\frac{\Delta \varphi }{\Delta t}=\frac{\varphi -{\varphi }_0}{t-t_0};$ ⇒ \omega = \frac{\varphi}{t};$\omega =\frac{\varphi }{t};$

Umlaufdauer T$T$: \omega = \frac{2\pi}{T}; \quad \left[T\right] = \mathrm{s};$\omega =\frac{2\pi }{T};\left[T\right]=\text{s};$

Frequenz f$f$: f = \frac{1}{T}; \quad \left[f\right] = \frac{1}{\mathrm{s}} = \mathrm{Hz};$f=\frac{1}{T};\left[f\right]=\frac{1}{\text{s}}=\text{Hz};$

⇒ \omega = 2 \pi f;$\omega =2\pi f;$

Bewegungsgleichungen:

• x(t) = r \cdot \cos \omega{}t;$x\left(t\right)=r\cdot cos\omega t;$

• y(t) = r \cdot \sin \omega{}t;$y\left(t\right)=r\cdot sin\omega t;$

Bahngeschwindigkeit: v = \frac{\varphi r}{t} = \frac{\omega t r}{t} = \omega r;$v=\frac{\varphi r}{t}=\frac{\omega tr}{t}=\omega r;$

Die Bahngeschwindigkeit ist tangential zum Kreis und steht senkrecht zum Ortsvektor \vec v$\overrightarrow{v}$.

Für die Ablenkung aus der geradlinigen Bahn ist (vgl. Trägheitssatz!) eine Kraft nötig. Bei einer Kreisbahn ist diese Kraft zum Kreismittelpunkt hin gerichtet und heißt Zentripetalkraft.

Gleichförmige Bewegung: \left| \vec v \right|$\left|\overrightarrow{v}\right|$ ändert sich nicht.

Symbol für die Zentripetalkraft: \vec F_r${\overrightarrow{F}}_r$

Nach Newton: \vec F_r = m \cdot \vec a_r;${\overrightarrow{F}}_r=m\cdot {\overrightarrow{a}}_r;$

Bestimmung der Zentripetalbeschleunigung \vec a_r${\overrightarrow{a}}_r$:

• Richtung von \vec a_r${\overrightarrow{a}}_r$: radial nach innen

• Betrag von \vec a_r${\overrightarrow{a}}_r$: \frac{\Delta\vec v}{\Delta t}$\frac{\Delta \overrightarrow{v}}{\Delta t}$: mittlere Beschleunigung im Zeitintervall \Delta t$\Delta t$

  \Delta t \to 0$\Delta t\to 0$ → Momentanbeschleunigung

  ⇒ \vec a_r = \lim\limits_{\Delta t \to 0} \frac{\Delta\vec v}{\Delta t};${\overrightarrow{a}}_r=\underset{\Delta t\to 0}{lim}\frac{\Delta \overrightarrow{v}}{\Delta t};$

  [Abb.]

  \vec v' = \vec v + \Delta\vec v;${\overrightarrow{v}}^{\prime }=\overrightarrow{v}+\Delta \overrightarrow{v};$

  Wegen ähnlicher Dreiecke folgt: \dfrac{\Delta v}{v} = \dfrac{\overline{PP'}}{r};$\frac{\Delta v}{v}=\frac{\overline{P{P}^{\prime }}}{r};$ ⇒ \Delta v = v \cdot \dfrac{\overline{PP'}}{r};$\Delta v=v\cdot \frac{\overline{P{P}^{\prime }}}{r};$ ⇒ \dfrac{\Delta v}{\Delta t} = \dfrac{v}{\Delta t} \dfrac{\overline{PP'}}{r};$\frac{\Delta v}{\Delta t}=\frac{v}{\Delta t}\frac{\overline{P{P}^{\prime }}}{r};$

  Mit \Delta t \to 0$\Delta t\to 0$ nähert sich \overline{PP'}$\overline{P{P}^{\prime }}$ der Bogenlänge \Delta s = v \cdot \Delta t$\Delta s=v\cdot \Delta t$ an.

  ⇒ \lim\limits_{\Delta t \to 0} \dfrac{\Delta v}{\Delta t} = \lim\limits_{\Delta t \to 0} \dfrac{v}{\Delta t} \dfrac{\overline{PP'}}{r}$\underset{\Delta t\to 0}{lim}\frac{\Delta v}{\Delta t}=\underset{\Delta t\to 0}{lim}\frac{v}{\Delta t}\frac{\overline{P{P}^{\prime }}}{r}$ "=$=$" \lim\limits_{\Delta t \to 0} \dfrac{v}{r} \dfrac{v \cdot \Delta t}{\Delta t} = \frac{v^2}{r} = \left|\vec a_r\right|;$\underset{\Delta t\to 0}{lim}\frac{v}{r}\frac{v\cdot \Delta t}{\Delta t}=\frac{v^2}{r}=\left|{\overrightarrow{a}}_r\right|;$

  Ergebnis: Für den Betrag der Zentripetalbeschleunigung bei der gleichförmigen Kreisbewegung gilt: \left|\vec a_r\right| = a_r = \frac{v^2}{r} = \omega^2 r;$\left|{\overrightarrow{a}}_r\right|=a_r=\frac{v^2}{r}={\omega }^{2}r;$

  Es gilt: a_r \sim r;$a_r\sim r;$

Folgerung: Für die Zentripetalkraft F_r$F_r$ gilt daher (nach NEWTONs 2. Gesetz): F_r = m \cdot a_r = m \frac{v^2}{r} = m \omega^2 r$F_r=m\cdot a_r=m\frac{v^2}{r}=m{\omega }^{2}r$ mit \omega = \frac{2\pi}{T};$\omega =\frac{2\pi }{T};$

[Versuch: Überprüfung unserer deduktiven Herleitung]

0.0.1.1 ↑ Beispiel: Schiffschaukel (vgl. Buch S. 89)

[Abbildung: Kreis, oben A, links B, unten C]

a)

In A$A$ soll v_A$v_A$ so groß sein, dass ein Gegenstand in der Schaukel nicht herunterfällt (Schwerelosigkeit), d.h. in A$A$ wird die Gewichtskraft komplett für die Zentripetalkraft verwendet:

F_{R_A} = F_G; \Rightarrow m\frac{v_A^2}{r} = mg; \Rightarrow v_A = \sqrt{rg};$F_{R_A}=F_G;\Rightarrow m\frac{v_A^2}{r}=mg;\Rightarrow v_A=\sqrt{rg};$

b)

Betrag der Geschwindigkeit auf dem Weg von A$A$ nach C$C$:

Energieerhaltung ⇒ \left|\vec v\right|$\left|\overrightarrow{v}\right|$ nimmt zu.

In C$C$: Nullniveau für E_{\mathrm{pot}}$E_{\text{pot}}$

Energiebilanz in der Höhe h$h$: 2mgr + \frac{1}{2}mv_A^2 = mgh + \frac{1}{2}mv_h^2; \Rightarrow v_h = \sqrt{5gr - 2gh};$2mgr+\frac{1}{2}m{v}_A^2=mgh+\frac{1}{2}m{v}_h^2;\Rightarrow v_h=\sqrt{5gr-2gh};$

Geschwindigkeit in B$B$: v_B = \sqrt{5gr - 2gr} = \sqrt{3gr}; \Rightarrow F_{R_B} = 3mg;$v_B=\sqrt{5gr-2gr}=\sqrt{3gr};\Rightarrow F_{R_B}=3mg;$

Geschwindigkeit in C$C$: v_C = \sqrt{5gr - 0} = \sqrt{5gr}; \Rightarrow F_{R_C} = 5mg;$v_C=\sqrt{5gr-0}=\sqrt{5gr};\Rightarrow F_{R_C}=5mg;$

0.0.1.2 ↑ Kurvenfahrt

F$F$: Kraft der Straße auf das Auto (Gegenkraft der Normalkraft)

Bei idealer Kuvenüberhöhung liefert \vec F + \vec G$\overrightarrow{F}+\overrightarrow{G}$ eine Kraft zum Mittelpunkt der Kreisbahn: \\ \vec F_r = \vec F + \vec G;${\overrightarrow{F}}_r=\overrightarrow{F}+\overrightarrow{G};$

Bei idealer Kurvenüberhöhung gilt:

\tan\alpha = \dfrac{F_r}{G} = \dfrac{m\frac{v^2}{r}}{mg} = \dfrac{v^2}{rg};$tan\alpha =\frac{F_r}{G}=\frac{m\frac{v^2}{r}}{mg}=\frac{v^2}{rg};$ (unabhängig von m$m$)

⇒ v = \sqrt{rg \cdot \tan\alpha}$v=\sqrt{rg\cdot tan\alpha }$ ist die optimale Geschwindigkeit für die Kurve.

0.0.1.3 ↑ Radler in der Kurve (ohne Überhöhung)

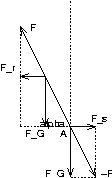
• Neigung nach innen um \alpha$\alpha$

• \vec F_r${\overrightarrow{F}}_r$: Zentripetalkraft

• \vec F_s${\overrightarrow{F}}_s$: Seitliche Kraft

• A$A$: Auflagepunkt

\vec F$\overrightarrow{F}$ ist die Reactio auf die Kraft des Rades im Auflagepunkt A$A$. Ihre Vertikalkomponente hält F_G$F_G$ das Gleichgewicht.

Die Horizontalkomponente von \vec F$\overrightarrow{F}$ ist \vec F_r${\overrightarrow{F}}_r$. Sie hat keine ersichtliche Gegenkraft¹ und dient als Zentripetalkraft.

Für den Neigungswinkel \alpha$\alpha$ gilt: \\\tan\alpha = \frac{F_r}{F_g} = \frac{v^2}{rg};$tan\alpha =\frac{F_r}{F_g}=\frac{v^2}{rg};$

In A$A$: F_s$F_s$ muss von der Haftung zwischen Reifen und Fahrbahn aufgebracht werden. Haftkraft F_H \geq F_s = F_r;$F_H\ge F_s=F_r;$

Wegen F_H = \mu \cdot F_s$F_H=\mu \cdot F_s$ folgt für die Haftreibungszahl: \\\mu \cdot F_G \geq F_r; \Rightarrow \mu \geq \frac{F_r}{F_G} = \tan\alpha;$\mu \cdot F_G\ge F_r;\Rightarrow \mu \ge \frac{F_r}{F_G}=tan\alpha ;$

Also sichere Kurvenfahrt, solange \mu > \tan\alpha;$\mu >tan\alpha ;$

0.0.1.4 ↑ Zwei Probleme

• Wie beeinflusst die Erdrotation die Gewichtskraft der Körper auf der Erdoberfläche (am Äquator, in Augsburg (48° n.Br.)) prozentual?

  F_r(\alpha) = m\dfrac{v^2}{r} = m\dfrac{v^2}{r\cos\alpha};$F_r\left(\alpha \right)=m\frac{v^2}{r}=m\frac{v^2}{rcos\alpha };$

  F_e(\alpha) = mg - F_R(\alpha) = m\left[g - \dfrac{v^2}{r\cos\alpha}\right];$F_e\left(\alpha \right)=mg-F_R\left(\alpha \right)=m\left[g-\frac{v^2}{rcos\alpha }\right];$

  \dfrac{F_e(\alpha)}{mg} = 1 - \dfrac{v^2}{rg\cos\alpha} = 1 - \dfrac{4\pi^2r^2}{rgT\cos\alpha} = 1 - \dfrac{4\pi^2r}{Tg\cos\alpha};$\frac{F_e\left(\alpha \right)}{mg}=1-\frac{v^2}{rgcos\alpha }=1-\frac{4{\pi }^2{r}^2}{rgTcos\alpha }=1-\frac{4{\pi }^{2}r}{Tgcos\alpha };$

  ⇒ Bei 0°: ca. 0,00343%\\$$ ⇒ Bei 48°: ca. 0,00513%

• Jeder Massenpunkt der Erdkugel, der nicht auf der Erdachse liegt, erfährt eine Zentrifugalkraft F_{fl} = m\omega^2R_E\cos\varphi$F_{fl}=m{\omega }^2{R}_{E}cos\varphi$. Sie ist senkrecht zur Erdachse gerichtet. F_{fl}$F_{fl}$ kann in zwei Komponenten zerlegt werden:

  • Die senkrecht zur Erdoberfläche gerichtete Radialkomponente F_{\mathrm{rad}}$F_{\text{rad}}$ -- Sie bewirkt...

  • Eine tangential zur Erdoberfläche (längs der Meridiane) verlaufende, zum Äquator gerichtete Tangentialkomponente F_{\mathrm{tang}}$F_{\text{tang}}$. Sie hat die Abplattung der Erde mit dem Wülsten am Äquator verursacht. (Die feste Erdkruste "schwimmt" auf einem flüssigen Kern!)